La funzione di passo di Heaviside è una funzione matematica denotata 
, o talvolta 
o 
(Abramowitz e Stegun 1972, p. 1020), e conosciuto anche come “funzione di passo unitario”. Il termine “funzione di passo di Heaviside” e il suo simbolo possono rappresentare sia una funzione costante piecewise che una funzione generalizzata.
Quando è definita come una funzione costante piecewise, la funzione di passo di Heaviside è data da
 |
(1)
|
(Abramowitz e Stegun 1972, p. 1020; Bracewell 2000, p. 61). Il grafico qui sopra mostra questa funzione (figura di sinistra), e come apparirebbe se visualizzata su un oscilloscopio (figura di destra).
Quando è definita come una funzione generalizzata, può essere definita come una funzione 
tale che
 |
(2)
|
per 
la derivata di una funzione sufficientemente liscia 
che decade sufficientemente rapidamente (Kanwal 1998).
Il linguaggio Wolfram rappresenta la funzione generalizzata di Heaviside come HeavisideTheta, mentre usa UnitStep per rappresentare la funzione piecewise Piecewise (che, va notato, adotta la convenzione 
invece della definizione convenzionale 
).
La notazione sintetica
 |
(3)
|
a volte viene anche usato.
La funzione di passo di Heaviside è legata alla funzione boxcar
 |
(4)
|
e può essere definito in termini di funzione segno da
 |
(5)
|
La derivata della della funzione di passo è data da
 |
(6)
|
dove 
è la funzione delta (Bracewell 2000, p. 97).
La funzione di passo di Heaviside è legata alla funzione di rampa 
da
 |
(7)
|
e alla derivata di 
da
 |
(8)
|
I due sono anche collegati attraverso
 |
(9)
|
dove 
indica la convoluzione.
Bracewell (2000) fornisce molte identità, alcune delle quali includono la seguente. Lasciando 
indicare la convoluzione,
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
Inoltre,
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
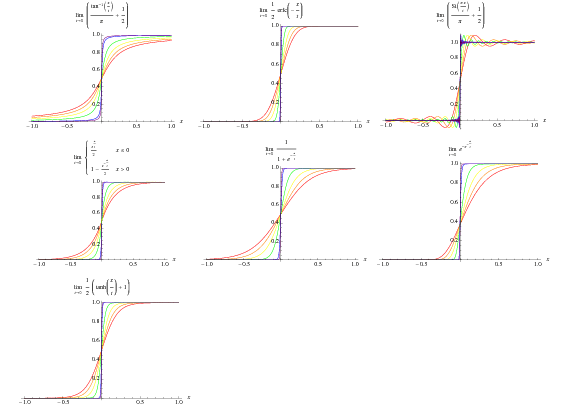
La funzione di Heaviside può essere definita dai seguenti limiti,
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
 |
 |
 |
(21)
|
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
(24)
|
|
 |
 |
 |
(25)
|
 |
 |
 |
(26)
|
 |
 |
 |
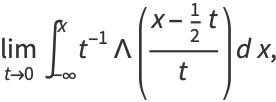(27)
|
dove 
è la funzione erfc, 
è l’integrale del seno, 
è la funzione sinc, e 
è la funzione triangolo a un argomento. Le prime quattro di queste sono illustrate sopra per 
, 0.1, e 0.01.
Ovviamente, qualsiasi funzione monotona con asintoti orizzontali costanti disuguali è una funzione a gradini di Heaviside sotto un appropriato ridimensionamento e un’eventuale riflessione. La trasformata di Fourier della funzione di passo di Heaviside è data da
 |
 |
 |
(28)
|
 |
 |
 |
(29)
|
dove 
è la funzione delta.