Goodness of Fit Test: Che cos’è?

Definizioni di statistica > Goodness of Fit Tests

La bontà del test di adattamento è usata per verificare se i dati del campione si adattano a una distribuzione di una certa popolazione (cioè una popolazione con una distribuzione normale o una con una distribuzione di Weibull).Cioè una popolazione con una distribuzione normale o una con una distribuzione di Weibull). In altre parole, vi dice se i vostri dati campione rappresentano i dati che vi aspettereste di trovare nella popolazione reale. I test di bontà di adattamento comunemente usati in statistica sono:

• il chi-quadro.
• Kolmogorov-Smirnov.
• Anderson-Darling.
• Shipiro-Wilk.

Il test della bontà del Chi Quadrato

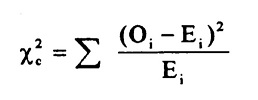
La formula del chi quadrato.

Il test del chi-quadrato è il più comune dei test di bontà dell’adattamento ed è quello che incontrerete nelle statistiche AP o nelle statistiche elementari. Il chi quadrato può essere usato per distribuzioni discrete come la distribuzione binomiale e la distribuzione di Poisson, mentre i test di Kolmogorov-Smirnov e Anderson-Darling possono essere usati solo per distribuzioni continue.

Due potenziali svantaggi del chi quadrato sono:

1. Il test chi quadrato può essere usato solo per dati messi in classi (bins). Se hai dati non suddivisi in bins avrai bisogno di fare una tabella di frequenza o un istogramma prima di eseguire il test.
2. Un altro svantaggio del test del chi-quadrato è che richiede una dimensione del campione sufficiente affinché l’approssimazione del chi-quadrato sia valida.

C’è un altro tipo di test del chi-quadrato, chiamato test del chi-quadrato per l’indipendenza. I due sono a volte confusi, ma sono abbastanza diversi.

• Il test del chi-quadrato per l’indipendenza confronta due serie di dati per vedere se c’è una relazione.
• Il test del chi-quadrato della bontà dell’adattamento consiste nell’adattare una variabile categorica a una distribuzione.

Entrambi i test usano la statistica del chi-quadrato e la distribuzione. Per maggiori informazioni sul calcolo della statistica del chi-quadrato, vedi:
La statistica del test del chi-quadrato (include i calcoli): Cos’è la statistica del chi-quadrato?

Eseguire il test

Tipo, questo test viene eseguito usando un software. L’ipotesi nulla per il test del chi-quadrato è che i dati provengano da una distribuzione specifica. L’ipotesi alternativa è che i dati non provengano da una distribuzione specifica.

Per interpretare il test, è necessario scegliere un livello alfa (1%, 5% e 10% sono comuni). Il test chi-quadro restituirà un valore p. Se il p-value è piccolo (meno del livello di significatività), puoi rifiutare l’ipotesi nulla che i dati provengano dalla distribuzione specificata.

Prove di adattamento meno comuni usate in statistica elementare

Kolmogorov-Smirnov

Anche se questo è chiamato un test di normalità, in realtà non ti dice se un particolare campione proviene da una popolazione normale. Invece, vi dirà quando è improbabile che si abbia una distribuzione normale. Un vantaggio di questo test è che non fa alcuna ipotesi sulla distribuzione dei dati. Un campione può essere confrontato con una distribuzione usando un test K-S a un campione o un test K-S a due campioni. Il test viene solitamente eseguito utilizzando un software (come SPSS), perché i valori critici devono essere calcolati per ogni distribuzione e trovare le tabelle dei valori critici non è un compito facile. Il test è solitamente raccomandato per grandi campioni oltre 2000. Per campioni più piccoli, usare Shapiro-Wilk.

Anderson-Darling

Questo test è una modifica di Kolmogorov-Smirnov. È più sensibile alle deviazioni nelle code di una distribuzione. Come il Kolmogorov-Smirnov, questo test vi dirà quando è improbabile che abbiate una distribuzione normale e viene normalmente eseguito utilizzando un software statistico.

Shapiro-Wilk

Questo test calcola un valore W che vi dirà se un campione casuale proviene da una popolazione distribuita normalmente. Il test è raccomandato per campioni fino a n=2000.

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 e 571, 2002.
Dodge, Y. (2008). L’enciclopedia concisa della statistica. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Vogt, W.P. (2005). Dictionary of Statistics & Metodologia: A Nontechnical Guide for the Social Sciences. SAGE.

——————————————————————————

Hai bisogno di aiuto per un compito a casa o per un test? Con Chegg Study, puoi ottenere soluzioni passo dopo passo alle tue domande da un esperto del settore. I tuoi primi 30 minuti con un tutor Chegg sono gratuiti!