Una matrice 
è una matrice ortogonale se
 |
(1)
|
dove 
è la trasposizione di 
e 
è la matrice identità. In particolare, una matrice ortogonale è sempre invertibile, e
 |
(2)
|
In forma di componente,
 |
(3)
|
Questa relazione rende le matrici ortogonali particolarmente facili da calcolare, poiché l’operazione di trasposizione è molto più semplice del calcolo dell’inverso.
Per esempio,
 |
 |
 |
(4)
|
 |
 |
 |
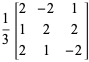(5)
|
sono matrici ortogonali.
Una matrice 
può essere testata per vedere se è ortogonale nel Wolfram Language usando OrthogonalMatrixQ.
Le righe di una matrice ortogonale sono una base ortonormale. Cioè, ogni riga ha lunghezza uno e sono reciprocamente perpendicolari. Allo stesso modo, anche le colonne sono una base ortonormale. Infatti, data una qualsiasi base ortonormale, la matrice le cui righe sono quella base è una matrice ortogonale. È automaticamente il caso che le colonne siano un’altra base ortonormale.
Le matrici ortogonali sono precisamente quelle matrici che conservano il prodotto interno
 |
(6)
|
Anche, il determinante di 
è o 1 o 
. Come sottoinsieme di 
, le matrici ortogonali non sono collegate poiché il determinante è una funzione continua. Invece, ci sono due componenti corrispondenti al fatto che il determinante sia 1 o 
. Le matrici ortogonali con 
sono rotazioni, e tale matrice è chiamata matrice ortogonale speciale.
Il prodotto matriciale di due matrici ortogonali è un’altra matrice ortogonale. Inoltre, l’inverso di una matrice ortogonale è una matrice ortogonale, così come la matrice identità. Quindi l’insieme delle matrici ortogonali forma un gruppo, chiamato gruppo ortogonale 
.