Po przeczytaniu tego rozdziału będziesz w stanie wykonać następujące czynności:
- Zdefiniować błąd losowy i odróżnić go od błędu systematycznego
- Przedstawić błąd losowy na przykładach
- Zinterpretować wartość p-
- Zinterpretuj przedział ufności
- Różnicuj pomiędzy błędami statystycznymi typu 1 i typu 2 i wyjaśnij, w jaki sposób odnoszą się one do badań epidemiologicznych
- Opisać, w jaki sposób moc statystyczna wpływa na badania
W tym rozdziale, omówimy błąd losowy – skąd się bierze, jak sobie z nim radzimy i co oznacza dla epidemiologii.
Po pierwsze i najważniejsze, błąd losowy nie jest błędem systematycznym. Bias jest błędem systematycznym i został omówiony bardziej szczegółowo w rozdziale 6.
Błąd losowy jest tym, czym brzmi: przypadkowymi błędami w danych. Wszystkie dane zawierają błędy losowe, ponieważ żaden system pomiarowy nie jest doskonały. Wielkość błędów losowych zależy częściowo od skali, w której coś jest mierzone (błędy w pomiarach na poziomie molekularnym byłyby rzędu nanometrów, podczas gdy błędy w pomiarach wzrostu człowieka są prawdopodobnie rzędu centymetra lub dwóch), a częściowo od jakości używanych narzędzi. Fizyczne i chemiczne laboratoria mają bardzo dokładne, drogie wagi, które mogą mierzyć masę z dokładnością do grama, mikrograma lub nanograma, podczas gdy przeciętna waga w czyjejś łazience jest prawdopodobnie dokładna do pół funta lub funta.
Aby owinąć głowę wokół przypadkowego błędu, wyobraź sobie, że pieczesz ciasto, które wymaga 6 łyżek masła. Aby uzyskać 6 łyżek masła (trzy czwarte kija, jeśli w funcie są 4 kije, jak to zwykle bywa w USA), możesz użyć oznaczeń, które pojawiają się na woskowanym papierze wokół kija, zakładając, że są one wyłożone prawidłowo. Możesz też zastosować metodę mojej mamy, która polega na rozpakowaniu patyczka, zrobieniu delikatnego znaku w miejscu, które wygląda jak połowa patyczka, a następnie dojściu do trzech czwartych poprzez zauważenie połowy tej połowy. Możesz też użyć mojej metody, która polega na zaznaczeniu wzrokiem trzech czwartych od początku i odciąć. Każda z tych metod „pomiaru” da Ci około 6 łyżek masła, co z pewnością wystarczy do upieczenia ciasta, ale prawdopodobnie nie dokładnie 3 uncje, czyli tyle, ile waży 6 łyżek masła w USA. Stopień, w jakim nieco przekroczyłeś 3 uncje tym razem i być może nieco poniżej 3 uncji następnym razem, jest spowodowany przypadkowym błędem w pomiarze masła. Jeśli zawsze niedoszacowałeś lub zawsze przeszacowywałeś, to byłby to błąd systematyczny – jednak twoje konsekwentnie niedoszacowane lub przeszacowane pomiary zawierałyby w sobie błąd losowy.
Dla dowolnej zmiennej, którą moglibyśmy chcieć zmierzyć w epidemiologii (np, wzrost, GPA, częstość akcji serca, liczba lat pracy w danej fabryce, poziom trójglicerydów w surowicy, itp.), spodziewamy się zmienności w próbie – to znaczy, nie oczekujemy, że każdy w populacji będzie miał dokładnie taką samą wartość. To nie jest błąd losowy. Błąd losowy (i stronniczość) pojawia się, gdy próbujemy zmierzyć te rzeczy. W rzeczywistości epidemiologia jako dziedzina opiera się na tej nieodłącznej zmienności. Gdyby wszyscy byli dokładnie tacy sami, nie bylibyśmy w stanie określić, które rodzaje ludzi są bardziej narażone na ryzyko rozwoju danej choroby.
W epidemiologii, czasami nasze pomiary polegają na człowieku innym niż uczestnik badania, mierzącym coś na lub o uczestniku. Przykłady obejmują pomiar wzrostu lub wagi, ciśnienia krwi lub stężenia cholesterolu w surowicy. W przypadku niektórych z nich (np. waga i cholesterol w surowicy) błąd losowy wkrada się do danych z powodu używanego instrumentu – tutaj, wagi, która ma prawdopodobnie półkilogramowe wahania, lub testu laboratoryjnego z marginesem błędu kilku miligramów na decylitr. W przypadku innych pomiarów (np. wzrostu i ciśnienia krwi), osoba dokonująca pomiaru jest odpowiedzialna za wszelkie przypadkowe błędy, jak w przykładzie z masłem.
Jednakże, wiele z naszych pomiarów polega na samo-raportowaniu się uczestników.
Jest wiele podręczników i zajęć poświęconych projektowaniu kwestionariuszy, a nauka o tym, jak uzyskać najdokładniejsze dane od ludzi za pomocą metod ankietowych jest całkiem dobra. Pew Research Center oferuje na swojej stronie internetowej przyjemny samouczek dotyczący projektowania kwestionariuszy.
W odniesieniu do naszej dyskusji, w danych kwestionariuszowych pojawią się również przypadkowe błędy. Dla niektórych zmiennych błąd losowy będzie mniejszy niż dla innych (np. podawana przez respondenta rasa jest prawdopodobnie dość dokładna), ale nadal będzie występował – na przykład, gdy respondent przypadkowo zaznaczy niewłaściwe pole. W przypadku innych zmiennych będzie więcej błędów losowych (np. nieprecyzyjne odpowiedzi na pytania takie jak: „Ile razy w ciągu ostatniego roku w miesiącu jadł(a) Pan(i) ryż?”). Dobrym pytaniem, które należy sobie zadać, rozważając wielkość błędu losowego, który może występować w zmiennej pochodzącej z kwestionariusza, jest pytanie: „Czy ludzie mogą mi to powiedzieć?”. Większość ludzi może teoretycznie powiedzieć, ile snu przespali ostatniej nocy, ale ciężko byłoby im powiedzieć, ile snu przespali tej samej nocy rok temu. To, czy powiedzą, czy nie, jest inną sprawą i dotyczy uprzedzeń (patrz rozdział 6).
Kwantyfikacja błędu losowego
Mimo że możemy – i powinniśmy – pracować nad zminimalizowaniem błędu losowego (używając wysokiej jakości narzędzi, szkoląc personel jak dokonywać pomiarów, projektując dobre kwestionariusze, itp. Na szczęście możemy wykorzystać statystykę do ilościowego określenia błędów losowych występujących w badaniu. W istocie do tego właśnie służy statystyka. W tej książce zajmę się tylko niewielkim wycinkiem rozległej dziedziny statystyki: interpretacją wartości p i przedziałów ufności (CI). Zamiast skupiać się na tym, jak je obliczać, skoncentruję się na tym, co one oznaczają (i czego nie oznaczają). Znajomość p-wartości i CI jest wystarczająca, aby umożliwić prawidłową interpretację wyników badań epidemiologicznych początkującym studentom epidemiologii.
p-wartości
Prowadząc badania naukowe każdego rodzaju, w tym epidemiologiczne, zaczynamy od postawienia hipotezy, która jest następnie testowana w miarę prowadzenia badania. Na przykład, jeśli badamy średni wzrost studentów studiów licencjackich, nasza hipoteza (zwykle oznaczona jako H1) może być taka, że studenci płci męskiej są średnio wyżsi niż studenci płci żeńskiej. Jednakże, dla celów testów statystycznych, musimy przeformułować naszą hipotezę jako hipotezę zerową. W tym przypadku nasza hipoteza zerowa (zwykle oznaczana jako H0) byłaby następująca:
Podejmujemy następnie nasze badanie w celu sprawdzenia tej hipotezy. Najpierw określamy populację docelową (studenci studiów licencjackich) i losujemy z niej próbę. Następnie mierzymy wysokość i płeć wszystkich osób w próbie i obliczamy średnią wysokość wśród mężczyzn w stosunku do wysokości wśród kobiet. Następnie przeprowadzamy test statystyczny, aby porównać średnie wysokości w tych dwóch grupach. Ponieważ mamy zmienną ciągłą (wzrost) mierzoną w 2 grupach (mężczyzn i kobiet), użylibyśmy testu t, a statystyka t obliczona za pomocą tego testu miałaby odpowiadającą jej wartość p, czyli to, na czym nam naprawdę zależy.
Powiedzmy, że w naszym badaniu stwierdzamy, że średnia wzrostu mężczyzn wynosi 5 stóp 10 cali, a wśród studentek średnia wysokość wynosi 5 stóp 6 cali (dla różnicy 4 cali), i obliczamy wartość p równą 0,04. Oznacza to, że jeśli naprawdę nie ma różnicy w średnim wzroście między studentami płci męskiej i studentkami (tzn. jeśli hipoteza zerowa jest prawdziwa) i powtórzymy badanie (aż do wylosowania nowej próbki z populacji), istnieje 4% szans, że ponownie znajdziemy różnicę w średnim wzroście wynoszącą 4 cale lub więcej.
Jest kilka implikacji wynikających z powyższego akapitu. Po pierwsze, w epidemiologii zawsze obliczamy 2-ogonowe p-wartości. W tym przypadku oznacza to po prostu, że 4% szans na ≥4-calową różnicę wzrostu nie mówi nic o tym, która grupa jest wyższa – po prostu jedna grupa (mężczyźni lub kobiety) będzie wyższa średnio o co najmniej 4 cale. Po drugie, p-wartości są bez znaczenia, jeśli zdarzy się, że do badania uda się włączyć całą populację. Na przykład, powiedzmy, że nasze pytanie badawcze dotyczy studentów z przedmiotu Zdrowie Publiczne 425 (H425, Podstawy epidemiologii) w semestrze zimowym 2020 na Uniwersytecie Stanowym w Oregonie (OSU). Czy w tej populacji wyżsi są mężczyźni czy kobiety? Ponieważ populacja jest dość mała, a wszyscy członkowie są łatwo identyfikowani, możemy zapisać wszystkich zamiast polegać na próbce. Nadal będzie istniał błąd losowy w pomiarze wzrostu, ale nie będziemy już używać wartości p do jego określenia. Dzieje się tak dlatego, że gdybyśmy mieli powtórzyć badanie, stwierdzilibyśmy dokładnie to samo, ponieważ zmierzyliśmy wszystkich w populacji. Wartości p mają zastosowanie tylko wtedy, gdy pracujemy z próbkami.
Na koniec zauważ, że wartość p opisuje prawdopodobieństwo twoich danych, zakładając, że hipoteza zerowa jest prawdziwa – nie opisuje ona prawdopodobieństwa, że hipoteza zerowa jest prawdziwa, biorąc pod uwagę twoje dane. Jest to częsty błąd interpretacyjny popełniany zarówno przez początkujących, jak i starszych czytelników badań epidemiologicznych. Wartość p nie mówi nic o tym, jak prawdopodobne jest, że hipoteza zerowa jest prawdziwa (a zatem, po przeciwnej stronie, o prawdziwości hipotezy rzeczywistej). Określa ona raczej prawdopodobieństwo uzyskania danych, które uzyskano, jeśli hipoteza zerowa okazała się prawdziwa. Jest to subtelne rozróżnienie, ale bardzo ważne.
Ważność statystyczna
Co dalej? Mamy wartość p, która mówi nam, jaka jest szansa na uzyskanie naszych danych przy hipotezie zerowej. Ale co to właściwie oznacza w kontekście tego, co należy wnioskować o wynikach badania? W badaniach z zakresu zdrowia publicznego i badań klinicznych standardową praktyką jest stosowanie wartości p ≤ 0,05 do oznaczania istotności statystycznej. Innymi słowy, dziesiątki lat badacze w tej dziedzinie wspólnie zdecydowali, że jeśli szansa popełnienia błędu typu I (więcej na ten temat poniżej) wynosi 5% lub mniej, to „odrzucimy hipotezę zerową”. Kontynuując przykład wzrostu z góry, doszlibyśmy zatem do wniosku, że istnieje różnica w wysokości pomiędzy płciami, przynajmniej wśród studentów studiów licencjackich. Dla wartości p powyżej 0,05 „nie odrzucamy hipotezy zerowej” i zamiast tego stwierdzamy, że nasze dane nie dostarczyły dowodów na istnienie różnicy wzrostu między mężczyznami i kobietami wśród studentów studiów licencjackich.
Jeśli p > 0,05, nie odrzucamy hipotezy zerowej. Nie przyjmujemy nigdy hipotezy zerowej, ponieważ bardzo trudno jest udowodnić brak czegoś. „Przyjęcie” hipotezy zerowej sugeruje, że udowodniliśmy, że naprawdę nie ma różnicy wzrostu między studentami płci męskiej i żeńskiej, co nie jest tym, co się stało. Jeśli p > 0.05, oznacza to jedynie, że nie znaleźliśmy dowodów przeciwnych do hipotezy zerowej – nie, że wspomniane dowody nie istnieją. Mogliśmy dostać dziwną próbkę, mogliśmy mieć zbyt małą próbkę, itd. Istnieje cała dziedzina badań klinicznych (badania porównawcze skutecznościvi) poświęcona wykazaniu, że jedno leczenie nie jest lepsze lub gorsze od drugiego; metody w tej dziedzinie są złożone, a wymagane wielkości prób są dość duże. W przypadku większości badań epidemiologicznych po prostu trzymamy się tego, aby nie odrzucić.
Czy wartość graniczna p ≤ 0,05 jest arbitralna? Absolutnie. Warto o tym pamiętać, szczególnie w przypadku wartości p bardzo blisko tego odcięcia. Czy 0,49 naprawdę tak bardzo różni się od 0,51? Prawdopodobnie nie, ale znajdują się one po przeciwnych stronach tej arbitralnej linii. Wielkość wartości p zależy od 3 rzeczy: wielkości próbki, wielkości efektu (łatwiej jest odrzucić hipotezę zerową, jeśli prawdziwa różnica wzrostu – gdybyśmy mierzyli wszystkich w populacji, a nie tylko naszą próbkę – wynosi 6 cali, a nie 2 cale) i spójności danych, najczęściej mierzonej odchyleniami standardowymi wokół średnich wysokości w 2 grupach. Tak więc wartość p równa 0,51 prawie na pewno mogłaby być mniejsza, gdybyśmy po prostu włączyli do badania więcej osób (dotyczy to mocy, która jest odwrotnością błędu typu II, omówionego poniżej). Ważne jest, aby pamiętać o tym fakcie, kiedy czyta się badania.
Testowanie istotności statystycznej jest częścią gałęzi statystyki zwanej statystyką częstości.ii Chociaż jest to niezwykle powszechne w epidemiologii i dziedzinach pokrewnych, praktyka ta nie jest ogólnie uważana za idealną naukę z wielu powodów. Po pierwsze i najważniejsze, wartość graniczna 0,05 jest całkowicie arbitralna,iii a ścisłe testy istotności odrzuciłyby wartość zerową dla p = 0,049, ale nie odrzuciłyby dla p = 0,051, mimo że są one niemal identyczne. Po drugie, istnieje o wiele więcej niuansów w interpretacji wartości p i przedziałów ufności niż te, które omówiłem w tym rozdziale.iv Na przykład, wartość p jest tak naprawdę testem wszystkich założeń analizy, a nie tylko hipotezy zerowej, a duża wartość p często wskazuje jedynie na to, że dane nie są w stanie rozróżnić wielu konkurujących ze sobą hipotez. Jednakże, ponieważ zarówno zdrowie publiczne, jak i medycyna kliniczna wymagają decyzji typu „tak lub nie” (Czy powinniśmy wydać środki na tę kampanię edukacji zdrowotnej? Czy ten pacjent powinien otrzymać ten lek?), musi istnieć jakiś system podejmowania decyzji „tak” lub „nie”, a test istotności statystycznej jest obecnie takim systemem. Istnieją inne sposoby kwantyfikacji błędu losowego i rzeczywiście statystyka bayesowska (która zamiast odpowiedzi „tak” lub „nie” daje prawdopodobieństwo, że coś się wydarzy)ii staje się coraz bardziej popularna. Niemniej jednak, jako że statystyka częstościowa i testowanie hipotez zerowych są nadal zdecydowanie najczęstszymi metodami stosowanymi w literaturze epidemiologicznej, to właśnie na nich skupimy się w tym rozdziale.
Błędy typu I i typu II
Błąd typu I (zwykle symbolizowany przez α, grecką literę alfa, i blisko związany z wartościami p) jest prawdopodobieństwem, że błędnie odrzucimy hipotezę zerową – innymi słowy, że „znajdziemy” coś, czego tak naprawdę nie ma. Wybierając 0,05 jako granicę istotności statystycznej, w dziedzinie zdrowia publicznego i badań klinicznych milcząco zgodziliśmy się, że jesteśmy gotowi zaakceptować fakt, że 5% naszych ustaleń będzie w rzeczywistości błędami typu I lub fałszywymi pozytywami.
Błąd typu II (zwykle symbolizowany przez β, grecką literę beta) jest przeciwieństwem: β jest prawdopodobieństwem, że nieprawidłowo nie odrzucisz hipotezy zerowej – innymi słowy, przeoczysz coś, co naprawdę tam jest.
Moc w badaniach epidemiologicznych jest bardzo różna: idealnie powinna wynosić co najmniej 90% (co oznacza, że współczynnik błędu typu II wynosi 10%), ale często jest znacznie niższa. Moc jest proporcjonalna do wielkości próby, ale w sposób wykładniczy – moc rośnie wraz ze wzrostem wielkości próby, ale przejście z 90 do 95% mocy wymaga znacznie większego skoku w wielkości próby niż przejście z 40 do 45% mocy. Jeśli w badaniu nie uda się odrzucić hipotezy zerowej, ale dane wyglądają tak, jakby istniała duża różnica między grupami, często problem polega na tym, że badanie było zbyt słabe, a przy większej próbie wartość p prawdopodobnie spadłaby poniżej magicznej wartości odcięcia 0,05. Z drugiej strony, część problemu z małymi próbkami polega na tym, że możesz przypadkowo otrzymać niereprezentatywną próbkę, a dodanie dodatkowych uczestników nie spowoduje, że wyniki będą istotne statystycznie. Załóżmy na przykład, że ponownie interesują nas różnice wzrostu związane z płcią, ale tym razem tylko wśród sportowców szkół wyższych. Zaczynamy od bardzo małego badania – tylko jedna drużyna męska i jedna drużyna żeńska. Jeśli wybierzemy, powiedzmy, męską drużynę koszykówki i żeńską drużynę gimnastyczną, prawdopodobnie znajdziemy ogromną różnicę średniego wzrostu – być może 18 cali lub więcej. Dodanie innych drużyn do naszego badania prawie na pewno spowodowałoby znacznie mniejszą różnicę w średnich wysokościach, a 18-calowa różnica „znaleziona” w naszym początkowym małym badaniu nie utrzymałaby się z czasem.
Odstępy ufności
Ponieważ ustaliliśmy dopuszczalny poziom alfa na 5%, w epidemiologii i pokrewnych dziedzinach najczęściej używamy 95% przedziałów ufności (95% CI). Można użyć 95% CI do przeprowadzenia testów istotności: jeśli 95% CI nie zawiera wartości zerowej (0 dla różnicy ryzyka i 1.0 dla ilorazów szans, ilorazów ryzyka i ilorazów częstości), to p < 0.05, a wynik jest statystycznie istotny.
Chociaż 95% CI mogą być używane do testowania istotności, zawierają one znacznie więcej informacji niż tylko to, czy wartość p wynosi < 0.05 czy nie. Większość badań epidemiologicznych podaje 95% CI wokół każdego szacunku punktowego, który jest prezentowany. Prawidłowa interpretacja 95% CI jest następująca:
Możemy to również zobrazować wizualnie:
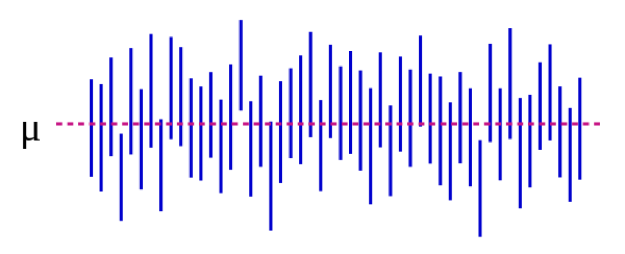
Źródło: https://es.wikipedia.org/wiki/Intervalo_de_confianza
Na rysunku 5-1 parametr populacji μ reprezentuje „prawdziwą” odpowiedź, którą otrzymalibyśmy, gdybyśmy mogli włączyć do badania absolutnie wszystkich w populacji. Oszacujemy μ na podstawie danych z naszej próby. Kontynuując nasz przykład wzrostu, może to być 5 cali: gdybyśmy mogli w magiczny sposób zmierzyć wzrost każdego studenta w USA (lub na świecie, w zależności od tego, jak zdefiniowaliśmy naszą populację docelową), średnia różnica między mężczyznami i kobietami wynosiłaby 5 cali. Co ważne, ten parametr populacji jest prawie zawsze nieobserwowalny – staje się on obserwowalny tylko wtedy, gdy definiujemy populację na tyle wąsko, że możemy włączyć do niej wszystkich. Każda niebieska pionowa linia reprezentuje CI pojedynczego „badania” – w tym przypadku 50 takich badań. CI różnią się, ponieważ próba jest za każdym razem nieco inna – jednak większość CI (wszystkie oprócz 3) zawiera μ.
Jeśli przeprowadzimy nasze badanie i stwierdzimy średnią różnicę 4 cali (95% CI, 1,5 – 7), CI powie nam dwie rzeczy. Po pierwsze, wartość p dla naszego testu t wyniosłaby <0.05, ponieważ CI wyklucza 0 (wartość zerową w tym przypadku, ponieważ obliczamy różnicę). Po drugie, interpretacja CI jest taka: jeśli powtórzylibyśmy nasze badanie (włączając w to losowanie nowej próbki) 100 razy, to 95 z tych razy nasze CI zawierałoby prawdziwą wartość (którą tutaj znamy jako 5 cali, ale której w prawdziwym życiu byśmy nie znali). Tak więc patrząc na CI wynoszące 1,5-7,0 cali można się zorientować, jaka może być rzeczywista różnica – prawie na pewno mieści się ona gdzieś w tym przedziale, ale może być tak mała jak 1,5 cala lub tak duża jak 7 cali. Podobnie jak p-wartości, CI zależą od wielkości próbki. Duża próba da względnie węższe CI. Węższe CI są uważane za lepsze, ponieważ dają bardziej precyzyjne oszacowanie tego, jaka może być „prawdziwa” odpowiedź.
Podsumowanie
Błąd losowy jest obecny we wszystkich pomiarach, chociaż niektóre zmienne są na niego bardziej podatne niż inne. Wartości P i CI są używane do ilościowego określenia błędu losowego. Wartość p równa 0,05 lub mniejsza jest zwykle uważana za „statystycznie istotną”, a odpowiadający jej współczynnik CI wyklucza wartość zerową. CI są przydatne do wyrażenia potencjalnego zakresu „prawdziwej” wartości na poziomie populacji, która jest szacowana.
i. Masło w USA i w pozostałej części świata. Errens Kitchen. Marzec 2014. https://www.errenskitchen.com/cooking-conversions/butter-measurement-weight-conversions/. Dostęp 26 września 2018. (↵ Powrót)
ii. Podejście bayesowskie vs frequentistyczne: te same dane, przeciwstawne wyniki. 365 Data Sci. sierpień 2017. https://365datascience.com/bayesian-vs-frequentist-approach/. Dostęp 17 października 2018 r. (↵ Zwrot 1) (↵ Zwrot 2)
iii. Smith RJ. The continuing misuse of null hypothesis significance testing in biological anthropology. Am J Phys Anthropol. 2018;166(1):236-245. doi:10.1002/ajpa.23399 (↵ Return)
iv. Farland LV, Correia KF, Wise LA, Williams PL, Ginsburg ES, Missmer SA. P-values i zdrowie reprodukcyjne: czego badacze kliniczni mogą nauczyć się od American Statistical Association? Hum Reprod Oxf Engl. 2016;31(11):2406-2410. doi:10.1093/humrep/dew192 (↵ Powrót)
v. Greenland S, Senn SJ, Rothman KJ, et al. Statistical tests, p values, confidence intervals, and power: a guide to misinterpretations. Eur J Epidemiol. 2016;31:337-350. doi:10.1007/s10654-016-0149-3
vi. Dlaczego badania porównawcze skuteczności są ważne? Patient-Centered Outcomes Research Institute. https://www.pcori.org/files/why-comparative-effectiveness-research-important. Dostęp 17 października 2018 r. (↵ Wróć)
- Nie ma tylko jednego wzoru na obliczenie wartości p lub CI. Wzory te zmieniają się w zależności od tego, jaki test statystyczny jest stosowany. Każdy tekst wprowadzający do biostatystyki, który omawia, jakie metody statystyczne należy stosować i kiedy, zawiera również odpowiednie informacje na temat obliczania p-wartości i CI. ↵
- Nie zastanawiaj się zbyt długo nad tym, dlaczego potrzebujemy hipotezy zerowej; po prostu ją potrzebujemy. Uzasadnienie jest zakopane w wiekach argumentów akademickiej filozofii nauki. ↵
- Jak wybrać właściwy test wykracza poza zakres tej książki – zobacz dowolną książkę na temat biostatystyki wprowadzającej ↵
Nieodłączny element wszystkich pomiarów. „Szum” w danych. Zawsze będzie obecny, ale jego ilość zależy od tego, jak precyzyjne są Twoje instrumenty pomiarowe. Na przykład, waga łazienkowa ma zazwyczaj 0,5 – 1 funt błędu przypadkowego; laboratoria fizyczne często posiadają wagi, które mają tylko kilka mikrogramów błędu przypadkowego (są one droższe i mogą ważyć tylko małe ilości). Można zmniejszyć ilość, o jaką błąd losowy wpływa na wyniki badań poprzez zwiększenie wielkości próbki. Nie eliminuje to błędu losowego, ale raczej pozwala badaczowi lepiej zobaczyć dane w szumie. Następstwo: zwiększenie liczebności próby spowoduje zmniejszenie wartości p i zawężenie przedziału ufności, ponieważ są to sposoby kwantyfikacji błędu losowego.
Błąd systematyczny. Błąd selekcji wynika z niewłaściwego doboru próby (próba nie jest reprezentatywna dla populacji docelowej), niskiego odsetka odpowiedzi od osób zaproszonych do udziału w badaniu, odmiennego traktowania przypadków i kontroli lub narażonych/nienarażonych i/lub nierównej utraty follow up między grupami. Aby ocenić stronniczość doboru, należy zadać sobie pytanie: „kogo udało się pozyskać, a kogo pominąć?” – a następnie zadać sobie pytanie: „czy to ma znaczenie”? Czasami ma, innym razem może nie ma.
Misclassification bias oznacza, że coś (albo ekspozycja, wynik, czynnik zakłócający, albo wszystkie trzy) zostało zmierzone niewłaściwie. Przykłady obejmują ludzi, którzy nie mogą ci czegoś powiedzieć, ludzi, którzy nie chcą ci czegoś powiedzieć, oraz obiektywny pomiar, który jest w jakiś sposób systematycznie błędny (np. zawsze w tym samym kierunku, jak mankiet do mierzenia ciśnienia krwi, który nie jest prawidłowo wyzerowany). Recall bias, social desirability bias, interviewer bias – to wszystko są przykłady błędnej klasyfikacji. Rezultatem końcowym wszystkich z nich jest to, że ludzie są umieszczani w niewłaściwych polach w tabeli 2×2. Jeśli błędna klasyfikacja jest równo rozłożona pomiędzy grupami (np. zarówno osoby narażone jak i nie narażone mają równe szanse na umieszczenie w niewłaściwej rubryce), jest to nieróżnicująca błędna klasyfikacja. W przeciwnym razie, jest to różnicowa błędna klasyfikacja.
Sposób kwantyfikacji błędu losowego. Prawidłowa interpretacja wartości p to: prawdopodobieństwo, że gdybyś powtórzył badanie (wrócił do populacji docelowej, wylosował nową próbkę, zmierzył wszystko, wykonał analizę), znalazłbyś wynik co najmniej tak samo skrajny, zakładając, że hipoteza zerowa jest prawdziwa. Jeśli w rzeczywistości prawdą jest, że nie ma różnicy między grupami, ale Twoje badanie wykazało, że w grupie A było o 15% więcej palaczy przy p-value równym 0,06, oznacza to, że istnieje 6% szans, że jeśli powtórzysz badanie, ponownie znajdziesz 15% (lub większą liczbę) palaczy więcej w jednej z grup. W badaniach z zakresu zdrowia publicznego i badań klinicznych zwykle używamy wartości granicznej p < 0,05, która oznacza „statystycznie istotny” – dopuszczamy więc 5% poziom błędu typu I. Tak więc, 5% czasu „znajdziemy” coś, nawet jeśli naprawdę nie ma różnicy (tj. nawet jeśli naprawdę hipoteza zerowa jest prawdziwa). W pozostałych 95% przypadków prawidłowo odrzucamy hipotezę zerową i stwierdzamy, że istnieje różnica między grupami.
Sposób kwantyfikacji błędu losowego. Prawidłowa interpretacja przedziału ufności brzmi: jeśli powtórzysz badanie 100 razy (wrócisz do populacji docelowej, pobierzesz nową próbkę, zmierzysz wszystko, wykonasz analizę), to 95 razy na 100 przedział ufności, który obliczysz w ramach tego procesu, będzie zawierał prawdziwą wartość, zakładając, że badanie nie zawiera błędu systematycznego. W tym przypadku prawdziwa wartość to ta, którą otrzymalibyśmy, gdybyśmy byli w stanie włączyć wszystkich z populacji do badania – prawie nigdy nie jest to faktycznie możliwe do zaobserwowania, ponieważ populacje są zazwyczaj zbyt duże, aby wszyscy mogli zostać włączeni do próbki. Następstwo: Jeśli Twoja populacja jest na tyle mała, że możesz mieć wszystkich w swoim badaniu, wtedy obliczanie przedziału ufności jest moot.
Używane w testowaniu istotności statystycznej. Hipotezą zerową jest zawsze brak różnicy między dwiema badanymi grupami.
Test statystyczny określający, czy wartości średnie w dwóch grupach są różne.
Nieco arbitralna metoda określania, czy wierzyć wynikom badania, czy nie. W badaniach klinicznych i epidemiologicznych istotność statystyczna jest zwykle ustalana na poziomie p < 0,05, co oznacza poziom błędu typu I <5%. Jak w przypadku wszystkich metod statystycznych, odnosi się tylko do błędu losowego; badanie może być statystycznie istotne, ale niewiarygodne, np. jeśli istnieje prawdopodobieństwo istotnej stronniczości. Badanie może być również istotne statystycznie (np. p było < 0,05), ale nieistotne klinicznie (np. jeśli różnica w skurczowym ciśnieniu krwi między dwiema grupami wynosiła 2 mm Hg – przy wystarczająco dużej próbie byłoby to istotne statystycznie, ale nie ma znaczenia klinicznego).
Prawdopodobieństwo, że badanie „znajdzie” coś, czego nie ma. Zazwyczaj reprezentowane przez α i ściśle związane z wartościami p. Zazwyczaj ustawiona na 0,05 dla badań klinicznych i epidemiologicznych.
Prawdopodobieństwo, że badanie znajdzie coś, co istnieje. Moc = 1 – β; beta to współczynnik błędu typu II. Małe badania lub badania rzadkich zdarzeń mają zwykle zbyt małą moc.
Prawdopodobieństwo, że badanie nie znajdzie czegoś, co istnieje. Zazwyczaj reprezentowane przez β i ściśle związane z mocą. W idealnych warunkach wynosi powyżej 90% dla badań klinicznych i epidemiologicznych, choć w praktyce często tak się nie dzieje.
Miara asocjacji, która jest obliczana w badaniu. Zazwyczaj przedstawiana z odpowiadającym jej 95% przedziałem ufności.