Wprowadzenie
Mierniki różnorodności alfa podsumowują strukturę społeczności ekologicznej w odniesieniu do jej bogactwa (liczba grup taksonomicznych), równomierności (rozkład liczebności grup), lub obu. Ponieważ wiele perturbacji w zbiorowisku wpływa na jego różnorodność alfa, podsumowywanie i porównywanie struktury zbiorowiska poprzez różnorodność alfa jest powszechnym podejściem do analizy badań zbiorowości. W ekologii mikroorganizmów, analiza różnorodności alfa danych z sekwencjonowania amplikonów jest powszechnym pierwszym podejściem do oceny różnic między środowiskami.
Niestety, określenie jak sensownie oszacować i porównać różnorodność alfa nie jest trywialne. Dla zilustrowania rozważmy następujący przykład, w którym metryką różnorodności alfa jest bogactwo na poziomie szczepów w społeczności mikrobiologicznej (całkowita liczba wariantów szczepów obecnych w środowisku). Załóżmy, że przeprowadzam eksperyment, w którym pobieram próbkę ze środowiska A i liczę liczbę różnych taksonów mikroorganizmów obecnych w mojej próbce. Następnie pobieram próbkę ze środowiska B, liczę liczbę różnych taksonów w tej próbce i porównuję ją z liczbą taksonów w środowisku A. Prawdopodobnie zaobserwuję większą liczbę różnych taksonów w próbce z większą liczbą odczytów mikrobiologicznych. Rozmiary bibliotek mogą zdominować biologię w określaniu wyniku analizy różnorodności (Lande, 1996).
Rarefaction jest metodą, która dostosowuje się do różnic w rozmiarach bibliotek w próbkach, aby pomóc w porównaniach różnorodności alfa. Po raz pierwszy zaproponowana przez Sandersa (1968), rafacja polega na wybraniu określonej liczby próbek, która jest równa lub mniejsza od liczby próbek w najmniejszej próbce, a następnie losowym odrzucaniu odczytów z większych próbek, aż liczba pozostałych próbek będzie równa temu progowi (patrz Hurlbert, 1971 dla wersji deterministycznej). W oparciu o te podpróbki o równej wielkości można obliczyć wskaźniki różnorodności, które mogą kontrastować ekosystemy „sprawiedliwie”, niezależnie od różnic w wielkości próbek (Weiss i in., 2017).
Niestety, rarefakcja nie jest ani uzasadniona, ani konieczna, co zostało ujęte statystycznie przez McMurdie i Holmesa (2014) w kontekście porównania względnych obfitości. W tym artykule omawiam, dlaczego nierówne liczebności prób wydają się powodować szczególne problemy w analizie różnorodności alfa. Wprowadzam statystyczną perspektywę szacowania różnorodności alfa i argumentuję, że powszechne spojrzenie na indeksy różnorodności powoduje fundamentalne problemy w porównywaniu próbek. Nie popierając żadnego konkretnego modelu pobierania próbek mikroorganizmów, sugeruję ogólne podejście do porównywania różnorodności mikrobiologicznej, takie, które uwzględnia niepewność w szacowaniu wskaźników różnorodności. Jednakże, ponieważ szacunki dla metryk różnorodności alfa są silnie zniekształcone, gdy taksony są nieobserwowane, nie powinno się porównywać różnorodności alfa używając danych surowych lub rastrowych. Opisuję metodologię statystyczną dla analizy różnorodności alfa, która uwzględnia brakujące taksony, która powinna być stosowana w miejsce istniejących powszechnych podejść do analizy różnorodności w ekologii. Chociaż w przykładach skupiam się na analizie danych mikrobiomowych, zagadnienia i dyskusja są w równym stopniu możliwe do zastosowania w analizie danych makroekologicznych. Co więcej, dyskusja ta odnosi się również do analiz różnorodności wykonywanych na poziomie szczepu, gatunku lub innym poziomie taksonomicznym.
Błąd pomiaru i wariancja w badaniach mikrobiomu
Wyobraźmy sobie, że posiadamy pełną wiedzę o każdym istniejącym mikrobie, łącznie z tożsamością, liczebnością i lokalizacją. Aby porównać różnorodność mikrobiomu, zdefiniowalibyśmy określone środowiska (np. dystalne jelita kobiet w wieku 35 lat mieszkających w sąsiednich Stanach Zjednoczonych) i porównalibyśmy wskaźniki różnorodności w różnych gradientach ekologicznych (np. z lub bez rozpoznania zespołu jelita drażliwego). Różnorodność alfa mogłaby być porównywana dokładnie, ponieważ znalibyśmy całe populacje mikroorganizmów z idealną precyzją.
Niestety, nie mamy wiedzy o każdym mikrobie. Pobieramy próbki z otoczenia i badamy społeczność mikrobiologiczną obecną w próbce. Używamy naszych ustaleń na temat próbki, aby wyciągnąć wnioski na temat środowiska, które nas naprawdę interesuje. Próbki nie są przedmiotem szczególnego zainteresowania, z wyjątkiem tego, że odzwierciedlają środowisko, z którego zostały pobrane. W miarę jak pobieramy coraz większe próbki środowiska, zbliżamy się do zrozumienia prawdziwej i całkowitej społeczności mikrobiologicznej, która nas interesuje. Oznacza to, że w miarę zwiększania próbkowania, nasze obliczenia jakiejkolwiek metryki różnorodności zbliżają się do wartości tej metryki obliczonej przy użyciu całej populacji.
Obserwacja małych próbek z dużej populacji nie jest eksperymentem unikalnym dla ekologii mikroorganizmów: jest niemal powszechna w statystyce. Sytuacja, w której oszacowanie wielkości zbiega się do poprawnej wartości w miarę uzyskiwania kolejnych próbek, jest również dobrze rozumiana w statystyce. Unikalną właściwością eksperymentów mikrobiomowych i analizy różnorodności alfa jest to, że próbki nie reprezentują wiernie całej badanej społeczności mikrobiologicznej. Używanie naszych próbek jako przybliżonych dla całej społeczności jest obarczone nieskorygowanym błędem.
Aby zilustrować to rozróżnienie, skontrastuję eksperymenty dotyczące różnorodności mikrobiomu z eksperymentem niemikrobiomowym. Załóżmy, że jesteśmy zainteresowani modelowaniem strumienia CO2 w glebie poddanej działaniu różnych poprawek. Zmierzylibyśmy strumień w miejscach o jednakowej wielkości, w których zastosowano różne poprawki, wykonując powtórzenia biologiczne w wielu miejscach dla każdej poprawki. Aby ocenić, czy poprawki wpływają na strumień, dopasowujemy model typu regresji (np. ANOVA) do strumienia z poprawką jako zmienną objaśniającą. Model ten zakłada, że możemy ocenić strumień z wysoką precyzją; to znaczy, że margines błędu przy określaniu strumienia jest nieistotny.
Załóżmy, że wiemy, że nasze urządzenie do pomiaru strumienia konsekwentnie zaniża strumień o dokładnie 5 jednostek. Dostosowalibyśmy się do błędu pomiarowego dodając 5 jednostek do każdego pomiaru przed ich porównaniem. Ale co się stanie, gdy będziemy mieli do czynienia z przypadkowym błędem pomiarowym? Jeśli błąd pomiarowy maszyny byłby losowy (np. ze średnią 0 i wariancją 1 jednostki dla wszystkich zmian), nie miałoby to wpływu na żadną konkretną zmianę. Jednakże, wykrycie różnicy pomiędzy wpływem poprawek na strumień byłoby trudniejsze statystycznie: potrzebowalibyśmy więcej próbek, aby wykryć prawdziwą różnicę w porównaniu do przypadku bez błędu pomiaru. Aby uwzględnić dodatkowy szum eksperymentalny, zastosowalibyśmy model, który uwzględniałby błąd pomiarowy w ocenie różnic między zmianami. Jeśli wariancja błędu pomiarowego wynosiłaby 1 jednostkę dla poprawki A, ale 5 jednostek dla poprawki B, w podobny sposób dokonalibyśmy korekty za pomocą modelu błędu pomiarowego.
Aby zdecydować, czy błąd pomiarowy musi być uwzględniony podczas obserwacji w eksperymencie, należy rozważyć efekt powtórzenia procesu obserwacyjnego na tej samej jednostce eksperymentalnej. W eksperymencie strumieniowym polegałoby to na ponownym pomiarze strumienia w tych samych miejscach gleby przy zastosowaniu tych samych warunków eksperymentalnych. Bez błędu pomiarowego w obserwacjach, konsekwentnie obserwowalibyśmy ten sam pomiar strumienia, podczas gdy gdybyśmy mieli losowy błąd pomiarowy, najprawdopodobniej obserwowalibyśmy nieco inne pomiary strumienia. Ponieważ repliki techniczne w eksperymentach mikrobiomowych dają różne liczby odczytów, różne składy społeczności i różne poziomy różnorodności alfa, w eksperymentach mikrobiomowych mamy do czynienia z błędem pomiaru. Obecnie nie uwzględniamy błędów pomiarowych w badaniach różnorodności mikrobiologicznej.
Bias w szacowaniu i porównywaniu różnorodności alfa
Pomimo, że błędy pomiarowe w badaniach mikrobiomu wpływają na wszystkie analizy danych mikrobiomu, różnorodność alfa jest szczególnie dotknięta, ponieważ powszechnie stosowane szacunki różnorodności alfa są silnie stronnicze w porównaniu z innymi problemami szacowania w ekologii mikrobiomu (takimi jak szacowanie względnych obfitości). Niektóre narzędzia do rozwiązywania problemów z tendencyjnością różnorodności alfa istnieją w literaturze statystycznej (Chao i Bunge, 2002; Willis i Bunge, 2015; Arbel et al., 2016; Willis i Martin, 2018). Istnieją jednak dwie nieprawidłowe praktyki otaczające różnorodność alfa, które uniemożliwiają upowszechnienie metodologii motywowanych statystycznie. Pierwszą praktyką jest używanie tendencyjnych oszacowań indeksów różnorodności alfa. Drugą praktyką jest traktowanie szacunków różnorodności alfa jako precyzyjnie obserwowanych wielkości, które nie są obarczone błędem pomiaru.
Aby wyjaśnić tę dyskusję, skupię się na bogactwie taksonomicznym (najprostszy przypadek), a później uogólnię argumentację na inne metryki różnorodności alfa. Rozważmy sytuację z Rysunku 1A, gdzie badamy dwa różne środowiska, a bogactwo środowiska A (nazwijmy je CA) jest wyższe niż bogactwo środowiska B (CB). Załóżmy, że mamy dwie repliki biologiczne próbek z każdego środowiska: nA1 i nA2 odczytów ze środowiska A, nB1 i nB2 odczytów ze środowiska B, oraz nA1 < nB1 < nA2 < nB2. Niech cij oznacza obserwowane bogactwo środowiska i na repliki j. Jak to może powszechnie występować w praktyce, cA1 < cA2 < cB1 < cB2.
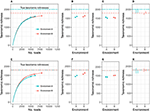
Figura 1. Oczekiwane bogactwo taksonomiczne próbki wzrasta wraz z liczbą odczytów (A,E). Porównywanie bogactwa taksonomicznego próbek może zatem często prowadzić do błędnych wniosków na temat prawdziwego bogactwa (B,F). Rarefying próbek do tej samej liczby odczytów może również prowadzić do błędnych wniosków (C,G). Dostosowanie dla nieobserwowanych taksonów i uwzględnienie niepewności w oszacowaniu prawidłowo wykrywa zarówno prawdziwe (D), jak i fałszywe (H) różnice w bogactwie. Chociaż przykład zastosowany tutaj dotyczy bogactwa mikrobiologicznego, ten sam argument ma zastosowanie do bogactwa makroekologicznego, jak również innych wskaźników różnorodności alfa.
W chwili obecnej istnieją dwie powszechnie stosowane metody porównywania różnorodności alfa. Pierwsza metoda, Rysunek 1B, polega na wykorzystaniu oszacowań cA1, cA2, cB1 i cB2 oraz przeprowadzeniu modelowania i testowania hipotez (takich jak ANOVA) tak, jakby zarówno skośność, jak i wariancja tych oszacowań wynosiły zero (zob. np. Makipaa i in., 2017). W przypadku rysunku 1A prowadzi to do błędnego wniosku, że środowisko A ma niższe bogactwo niż środowisko B. Druga metoda polega na wygenerowaniu znormalizowanej lub rzadkiej próbki poprzez losowe odrzucanie odczytów ze wszystkich próbek, aż każda próbka będzie miała nA1 odczytów (liczba odczytów w najmniejszej próbce), Rysunek 1C. Uzyskane w ten sposób rozproszone poziomy bogactwa to cA1, cA2′, cB1′ i cB2′. Oszacowania te są następnie wykorzystywane do modelowania i testowania hipotez (patrz np. Arora i in., 2017). Prowadzi to do wniosku, że środowisko A i środowisko B nie mają znacząco różnych bogactw, a szacunki bogactwa są znacznie poniżej rzeczywistych bogactw każdego ekosystemu (istnieje znaczna ujemna tendencyjność w szacunkach), co uniemożliwia porównanie bogactwa w różnych eksperymentach. Ponadto, nie wszystkie informacje zebrane w próbkach zostały wykorzystane do porównania.
W tym miejscu opowiadam się za trzecią strategią: dostosowanie próbkowego bogactwa każdego ekosystemu poprzez dodanie do niego oszacowania liczby nieobserwowanych gatunków, oszacowanie wariancji w całkowitym oszacowaniu bogactwa i porównanie zróżnicowania w odniesieniu do tych błędów (Rysunek 1D). Zaletą tej opcji jest wykorzystanie wszystkich obserwowanych odczytów, porównanie szacunków rzeczywistego parametru zainteresowania (bogactwa taksonomicznego) i uwzględnienie szumu eksperymentalnego. W przypadku, gdy środowiska mają równe bogactwo (Rysunki 1E-H), podejście to prawidłowo wykrywa równe bogactwo, nawet jeśli struktury obfitości różnią się.
Modelowanie parametrów obserwowanych z błędem estymacji nie jest nową sugestią: podejście to pochodzi z dziedziny metaanalizy statystycznej, gdzie porównuje się wyniki wielu badań szacujących tę samą wielkość efektu (Demidenko, 2004; Willis et al., 2016; Washburne et al., 2018). W metaanalizach większe badania muszą mieć większą wagę w określaniu ogólnej wielkości efektu, a to jest włączone do metaanalizy poprzez mniejsze błędy standardowe na szacunkach wielkości efektu. Podobnie, gdy porównuje się odpowiedź różnych grup leczenia w badaniach klinicznych, liczba uczestników w każdej grupie leczenia jest uwzględniana w porównaniu ogólnego efektu leczenia. Dostosowanie do wielkości próby podczas porównywania różnych grup obserwacji bez odrzucania danych jest szeroko rozpowszechnione w naukach ścisłych, a odrzucanie danych w celu dostosowania do nierównej wielkości próby jest wyjątkiem. Przedstawiona tutaj strategia modelowania bogactwa po skorygowaniu o brakujące gatunki koryguje zarówno błąd systematyczny, jak i wariancję, uwzględniając w ten sposób różnice w wielkości biblioteki i niekompletne badania mikrobiologiczne.
Pomimo, że omawiany tutaj przykład dotyczy bogactwa, to podejście do szacowania i porównywania różnorodności alfa z wykorzystaniem korekty błędu systematycznego (uwzględniającej nieobserwowane taksony) i korekty wariancji (model błędu pomiaru) można zastosować do każdej metryki różnorodności alfa. Jednakże, szacowanie bogactwa jest dobrze zbadane w literaturze statystycznej i istnieją estymatory bogactwa, które są dostosowane do danych mikrobiomu (patrz Bunge i in., 2014 w celu dokonania przeglądu). To samo nie jest prawdą w przypadku innych metryk różnorodności alfa. Na przykład, estymatory bogactwa taksonomicznego Chao-Bunge (Chao i Bunge, 2002) i breakaway (Willis i Bunge, 2015) dostarczają szacunków wariancji, uwzględniają nieobserwowane taksony i nie są zbyt wrażliwe na liczbę singletonów (liczba gatunków obserwowanych jeden raz). W przeciwieństwie do tego, estymator entropii dostosowany do pokrycia indeksu Shannona (Chao i Shen, 2003) dostarcza szacunków wariancji i uwzględnia nieobserwowane taksony, ale jest bardzo wrażliwy na liczbę pojedynczych osobników, która jest często trudna do określenia w badaniach mikrobiomów. Podczas gdy szacowanie różnorodności alfa dla mikrobiomów jest aktywnym obszarem badań w statystyce (Arbel i in., 2016; Zhang i Grabchak, 2016; Willis i Martin, 2018), pozostaje wiele cech ekosystemów mikrobiomu (takich jak przesłuch między próbkami i przestrzenna organizacja mikrobów), które nie zostały jeszcze włączone do metodologii statystycznej szacowania różnorodności alfa. Pomimo tego, szacunki różnorodności alfa, które uwzględniają nieobserwowane taksony i dostarczają szacunków wariancji, są znacznie lepsze zarówno od szacunków typu plug-in, jak i rarefied, które nie uwzględniają nieobserwowanych taksonów ani nie dostarczają szacunków wariancji.
Dyskusja
Oszacowania typu plug-in wielu wskaźników różnorodności alfa (w tym bogactwa i różnorodności Shannona) są ujemnie stronnicze dla parametru różnorodności alfa środowiska, czyli zaniżają prawdziwą różnorodność alfa (Lande, 1996). Próba rozwiązania tego problemu za pomocą rarefakcji w rzeczywistości indukuje większą tendencyjność. Jest to czasami usprawiedliwiane twierdzeniem, że szacunki z wykorzystaniem rastraty są równie tendencyjne. Jednak generalnie nie jest to prawdą, ponieważ środowiska mogą być identyczne pod względem jednej metryki różnorodności alfa, ale różne struktury liczebności będą powodować różne błędy przy rafacji. Na przykład, Rysunek 1E przedstawia dwa środowiska o różnych strukturach liczebności, ale równym bogactwie; rafying daje fałszywe wrażenie nierównego bogactwa (patrz też Lande i in., 2000). W ten sposób zarówno bogactwo próbki jak i bogactwo rafii są napędzane przez artefakty eksperymentu (rozmiar biblioteki), a nie wyłącznie przez strukturę społeczności mikrobiologicznej. Aby wyciągnąć znaczące wnioski na temat całej społeczności mikrobiologicznej, konieczne jest dostosowanie się do niewyczerpującego próbkowania przy użyciu statystycznie umotywowanych oszacowań parametrów dla różnorodności alfa. Aby wyciągnąć znaczące wnioski dotyczące porównań zbiorowisk drobnoustrojów, konieczne jest użycie modeli błędu pomiaru, aby dostosować się do niepewności w szacowaniu różnorodności alfa.
Ostatnio argumentowano, że studiowanie różnorodności drobnoustrojów bez kontekstu odciąga nas od uzyskania wglądu w mechanizmy ekologiczne (Shade, 2016). Do tej krytyki dodaję, że niewłaściwe stosowanie narzędzi statystycznych podważa wiele analiz różnorodności alfa. Zachęcam ekologów mikroorganizmów do stosowania oszacowań różnorodności alfa, które uwzględniają gatunki nieobserwowane, oraz do stosowania wariancji oszacowań w modelach błędu pomiaru w celu porównania różnorodności w różnych ekosystemach.
Wkład Autora
AW napisał manuskrypt i przeprowadził analizę danych.
Finansowanie
AW jest wspierany przez fundusze na rozpoczęcie działalności przyznane przez Departament Biostatystyki na Uniwersytecie Waszyngtońskim, oraz National Institutes of Health (R35GM133420).
Konflikt interesów
Autor oświadcza, że badania zostały przeprowadzone przy braku jakichkolwiek komercyjnych lub finansowych powiązań, które mogłyby być interpretowane jako potencjalny konflikt interesów.
Podziękowania
Ten artykuł jest oparty na notatkach z kursów przedstawionych przez autora w Marine Biological Laboratory na kursie STAMPS w 2013, 2014, 2015, 2016, 2017 i 2018 roku. Autor jest wdzięczny Berry’emu Brosi, MBL, dyrektorom kursu STAMPS i uczestnikom STAMPS za niezliczone dyskusje na ten temat. Autor dziękuje również Thea Whitman i dwóm recenzentom za wiele przemyślanych sugestii dotyczących manuskryptu. Ten manuskrypt został opublikowany jako preprint za pośrednictwem bioRxiv (Willis, 2017).
Arbel, J., Mengersen, K., and Rousseau, J. (2016). Bayesian nonparametric dependent model for partially replicated data: the influence of fuel spills on species diversity. Ann. Appl. Stat. 10, 1496-1516. doi: 10.1214/16-AOAS944
CrossRef Full Text | Google Scholar
Arora, T., Seyfried, F., Docherty, N. G., Tremaroli, V., le Roux, C. W., Perkins, R., et al. (2017). Diabetes-associated microbiota in fa/fa rats is modified by Roux-en-Y gastric bypass. ISME J. 11, 2035-2046. doi: 10.1038/ismej.2017.70
PubMed Abstract | CrossRef Full Text | Google Scholar
Bunge, J., Willis, A., and Walsh, F. (2014). Szacowanie liczby gatunków w badaniach różnorodności mikrobiologicznej. Annu. Rev. Stat. Appl. 1, 427-445. doi: 10.1146/annurev-statistics-022513-115654
CrossRef Full Text | Google Scholar
Chao, A., and Bunge, J. (2002). Oszacowanie liczby gatunków w stochastycznym modelu liczebności. Biometrics 58, 531-539. doi: 10.1111/j.0006-341X.2002.00531.x
PubMed Abstract | CrossRef Full Text | Google Scholar
Chao, A., and Shen, T.-J. (2003). Nonparametric estimation of Shannon’s index of diversity when there are unseen species in sample. Environ. Ecol. Stat. 10, 429-443. doi: 10.1023/A:1026096204727
CrossRef Full Text | Google Scholar
Demidenko, E. (2004). Mixed Models: Theory and Applications. Hoboken, NJ: Wiley-Interscience. doi: 10.1002/0471728438
CrossRef Full Text | Google Scholar
Fisher, R. A., Corbet, A. S., and Williams, C. B. (1943). The relationship between the number of species and the number of individuals in a random sample of an animal population. J. Anim. Ecol. 12:42. doi: 10.2307/1411
CrossRef Full Text | Google Scholar
Hurlbert, S. H. (1971). The nonconcept of species diversity: a critique and alternative parameters. Ecology 52, 577-586. doi: 10.2307/1934145
PubMed Abstract | CrossRef Full Text | Google Scholar
Lande, R. (1996). Statystyka i podział różnorodności gatunkowej, oraz podobieństwo między wieloma zbiorowiskami. Oikos 76, 5-13. doi: 10.2307/3545743
CrossRef Full Text | Google Scholar
Lande, R., DeVries, P. J., and Walla, T. R. (2000). When species accumulation curves intersect: implications for ranking diversity using small samples. Oikos 89, 601-605. doi: 10.1034/j.1600-0706.2000.890320.x
CrossRef Full Text | Google Scholar
Makipaa, R., Rajala, T., Schigel, D., Rinne, K. T., Pennanen, T., Abrego, N., et al. (2017). Interactions between soil- and dead wood-inhabiting fungal communities during the decay of Norway spruce logs. ISME J. 11, 1964-1974. doi: 10.1038/ismej.2017.57
PubMed Abstract | CrossRef Full Text | Google Scholar
McMurdie, P. J., and Holmes, S. (2014). Waste not, want not: dlaczego rarefying danych mikrobiomu jest niedopuszczalny. PLoS Comput. Biol. 10:e1003531. doi: 10.1371/journal.pcbi.1003531
CrossRef Full Text | Google Scholar
Sanders, H. L. (1968). Marine benthic diversity: a comparative study. Am. Nat. 102, 243-282. doi: 10.1086/282541
CrossRef Full Text | Google Scholar
Shade, A. (2016). Różnorodność jest pytaniem, a nie odpowiedzią. ISME J. 11, 1-6. doi: 10.1038/ismej.2016.118
CrossRef Full Text | Google Scholar
Shannon, C. E. (1948). Matematyczna teoria komunikacji. Bell Syst. Tech. J. 27, 379-423. doi: 10.1002/j.1538-7305.1948.tb01338.x
CrossRef Full Text | Google Scholar
Simpson, E. H. (1949). Pomiar różnorodności. Nature 163:688. doi: 10.1038/163688a0
CrossRef Full Text | Google Scholar
Washburne, A. D., Morton, J. T., Sanders, J., McDonald, D., Zhu, Q., Oliverio, A. M., et al. (2018). Metody analizy filogenetycznej danych mikrobiomu. Nat. Microbiol. 3:652. doi: 10.1038/s41564-018-0156-0
PubMed Abstract | CrossRef Full Text | Google Scholar
Weiss, S., Xu, Z. Z., Peddada, S., Amir, A., Bittinger, K., Gonzalez, A., et al. (2017). Normalization and microbial differential abundance strategies depend upon data characteristics. Microbiome 5:27. doi: 10.1186/s40168-017-0237-y
PubMed Abstract | CrossRef Full Text | Google Scholar
Willis, A. (2017). Rarefaction, alpha diversity, and statistics. bioRxiv 1-8. doi: 10.1101/231878
CrossRef Full Text | Google Scholar
Willis, A., and Bunge, J. (2015). Estymacja różnorodności poprzez współczynniki częstotliwości. Biometrics 71, 1042-1049. doi: 10.1111/biom.12332
PubMed Abstract | CrossRef Full Text | Google Scholar
Willis, A. D., Bunge, J., and Whitman, T. (2016). Ulepszone wykrywanie zmian w bogactwie gatunkowym w zbiorowiskach mikrobiologicznych o wysokiej różnorodności. J. R. Stat. Soc. C Appl. Stat. 66, 963-977. doi: 10.1111/rssc.12206
CrossRef Full Text | Google Scholar
Willis, A. D., and Martin, B. D. (2018). Divnet: estimating diversity in networked communities. bioRxiv 1-23. doi: 10.1101/305045
CrossRef Full Text | Google Scholar
Zhang, Z., and Grabchak, M. (2016). Entropiczna reprezentacja i estymacja indeksów różnorodności. J. Nonparametr. Stat. 28, 563-575. doi: 10.1080/10485252.2016.1190357
CrossRef Full Text | Google Scholar