Funkcja schodkowa Heaviside’a

Funkcja schodkowa Heaviside’a jest funkcją matematyczną oznaczaną , lub czasem lub (Abramowitz i Stegun 1972, s. 1020), a także znany jako „funkcja kroku jednostkowego”. Termin „funkcja stopnia Heaviside’a” i jej symbol mogą reprezentować albo funkcję stałą w pewnym sensie, albo funkcję uogólnioną.

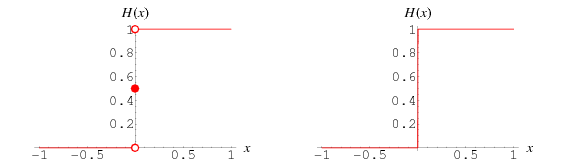
Gdy jest zdefiniowana jako funkcja stała, funkcja schodkowa Heaviside’a jest dana przez

(1)

(Abramowitz i Stegun 1972, s. 1020; Bracewell 2000, s. 61). Powyższy wykres przedstawia tę funkcję (lewy rysunek), oraz jak wyglądałaby ona po wyświetleniu na oscyloskopie (prawy rysunek).

Gdy jest zdefiniowana jako funkcja uogólniona, można ją zdefiniować jako funkcję taką, że

(2)

dla pochodna wystarczająco gładkiej funkcji która rozkłada się wystarczająco szybko (Kanwal 1998).

Język Wolframa reprezentuje uogólnioną funkcję Heaviside’a jako HeavisideTheta, podczas gdy używa UnitStep do reprezentowania funkcji Piecewise (która, należy zauważyć, przyjmuje konwencję zamiast konwencjonalnej definicji ).

Notacja skrótowa

(3)

Czasami stosuje się również.

Funkcja schodkowa Heaviside’a jest związana z funkcją boxcarfunction przez

(4)

i może być zdefiniować w kategoriach funkcji znaku przez

(5)

Pochodna funkcji kroku jest dana przez

(6)

gdzie jest funkcją delta (Bracewell 2000, str. 97).

Funkcja krokowa Heaviside’a jest związana z funkcją rampy przez

(7)

i do pochodnej przez

(8)

Dwa są również połączone przez

(9)

gdzie oznacza konwolucję.

Bracewell (2000) podaje wiele tożsamości, niektóre z nich są następujące. Niech oznacza konwolucję,

(10)

.

			(11)
			(12)
			(13)
			(14)

Dodatkowo,

.

			(15)
			(16)

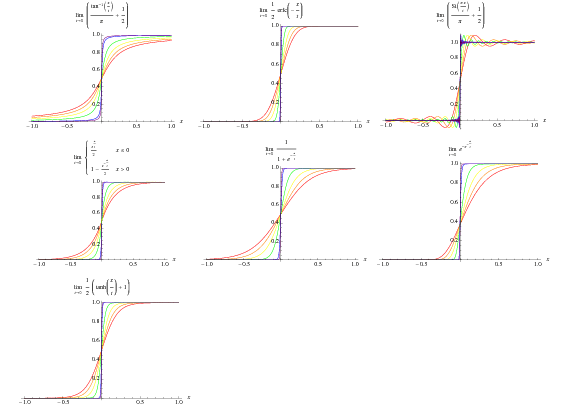
Funkcję schodkową Heaviside’a można zdefiniować za pomocą następujących granic,

			(17)
			(18)
			(19)
			(20)
			(21)
			(22)
			(23)
			(24)
			(25)
			(26)
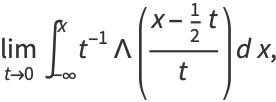			(27)

gdzie jest funkcją erfc, to całka sinus, to funkcja sinc, a to jednoargumentowa funkcja trójkąta. Pierwsze cztery z nich są zilustrowane powyżej dla , 0.1, i 0.01.

Oczywiście każda funkcja monotoniczna o stałych nierównych asymptotach poziomych jest funkcją schodkową Heaviside’a przy odpowiednim skalowaniu i ewentualnym odbiciu. Transformata Fouriera funkcji schodkowej Heaviside’a jest dana przez

			(28)
			(29)

gdzie jest funkcją delta.