Testowanie hipotez i przedziały ufnościEdit
Wartość P dla kappa jest rzadko podawana, prawdopodobnie dlatego, że nawet stosunkowo niskie wartości kappa mogą być znacząco różne od zera, ale nie na tyle duże, aby zadowolić badaczy.Niemniej jednak jej błąd standardowy został opisany i jest obliczany przez różne programy komputerowe.
Przedziały ufności dla Kappa można skonstruować dla oczekiwanych wartości Kappa, gdybyśmy mieli nieskończoną liczbę sprawdzanych pozycji, korzystając z następującego wzoru:
C I : κ ± Z 1 – α / 2 S E κ {displaystyle CI:\a_ppa \pm Z_{1-alfa /2}SE_{kappa }}

Gdzie Z 1 – α / 2 = 1,965 {displaystyle Z_{1-alfa /2}=1,965}

jest standardowym normalnym percentylem, gdy α = 5 % {{displaystyle Z_{1-alfa =5}}.

, a S E κ = p o ( 1 – p o ) N ( 1 – p e ) 2 {displaystyle SE_{kappa }={sqrt {{p_{o}(1-p_{o})}} \ponad {{N(1-p_{e})^{2}}}}}

Oblicza się to, ignorując fakt, że pe jest szacowane na podstawie danych, i traktując po jako szacowane prawdopodobieństwo rozkładu dwumianowego przy jednoczesnym zastosowaniu normalności asymptotycznej (tj.: zakładając, że liczba elementów jest duża i że po nie jest bliskie ani 0, ani 1). S E κ {{displaystyle SE_{kappa }}

(i CI w ogóle) można również oszacować za pomocą metod bootstrapowych.
Interpretacja magnitudeEdit

Jeśli istotność statystyczna nie jest użytecznym przewodnikiem, jaka wielkość kappa odzwierciedla odpowiednią zgodność? Wytyczne byłyby pomocne, ale czynniki inne niż porozumienie mogą wpływać na jego wielkość, co sprawia, że interpretacja danej wielkości jest problematyczna. Jak zauważyli Sim i Wright, dwoma ważnymi czynnikami są częstość występowania (czy kody są ekwiwalentne, czy też ich prawdopodobieństwa się różnią) oraz stronniczość (czy prawdopodobieństwa krańcowe dla dwóch obserwatorów są podobne, czy różne). Przy innych założeniach, kappas jest wyższe, gdy kody są ekwiwalentne. Z drugiej strony, kappas są wyższe, gdy kody są dystrybuowane asymetrycznie przez dwóch obserwatorów. W przeciwieństwie do zmian prawdopodobieństwa, efekt stronniczości jest większy, gdy Kappa jest mała niż gdy jest duża.:261-262
Kolejnym czynnikiem jest liczba kodów. Wraz ze wzrostem liczby kodów, kappas stają się wyższe. Na podstawie badania symulacyjnego Bakeman i współpracownicy doszli do wniosku, że dla zawodnych obserwatorów wartości kappa są niższe, gdy kodów jest mniej. I, w zgodzie z oświadczeniem Sima Wrights’a dotyczącym powszechności, kappas były wyższe, gdy kody były w przybliżeniu ekwiwalentne. Tak więc Bakeman et al. doszli do wniosku, że „żadna jedna wartość kappa nie może być uważana za uniwersalnie akceptowalną.”:357 Dostarczają oni również program komputerowy, który pozwala użytkownikom obliczyć wartości dla kappa określając liczbę kodów, ich prawdopodobieństwo i dokładność obserwatora. Na przykład, przy ekwiwalentnych kodach i obserwatorach, którzy są dokładni w 85%, wartości kappa wynoszą 0,49, 0,60, 0,66 i 0,69, gdy liczba kodów wynosi odpowiednio 2, 3, 5 i 10.
Niemniej jednak w literaturze pojawiły się wytyczne dotyczące wielkości. Być może pierwszymi byli Landis i Koch, którzy scharakteryzowali wartości < 0 jako wskazujące na brak porozumienia, 0-0,20 jako niewielkie, 0,21-0,40 jako sprawiedliwe, 0,41-0,60 jako umiarkowane, 0,61-0,80 jako znaczne, a 0,81-1 jako prawie doskonałe porozumienie. Ten zestaw wytycznych nie jest jednak w żaden sposób powszechnie akceptowany; Landis i Koch nie przedstawili żadnych dowodów na jego poparcie, opierając się zamiast tego na osobistej opinii. Zauważono, że te wytyczne mogą być bardziej szkodliwe niż pomocne. Równie arbitralne wytyczne Fleissa charakteryzują kappę powyżej 0,75 jako doskonałą, 0,40 do 0,75 jako dobrą do dobrej, a poniżej 0,40 jako słabą.
Kappa maksymalnaEdit
Kappa przyjmuje swoją teoretyczną maksymalną wartość 1 tylko wtedy, gdy obaj obserwatorzy rozdzielają kody tak samo, to znaczy, gdy odpowiadające im sumy wierszy i kolumn są identyczne. Cokolwiek mniej oznacza mniej niż doskonałą zgodność. Mimo to, maksymalna wartość kappa, jaką mogłaby osiągnąć przy nierównym rozkładzie, pomaga zinterpretować wartość kappa faktycznie uzyskaną. Równanie dla κ max jest następujące:
κ max = P max – P exp 1 – P exp {{displaystyle \amppa _{max }={frac {P_{max }-P_{exp }}{1-P_{exp }}}}


, jak zwykle, P max = ∑ i = 1 k min ( P i + , P + i ) {{displaystyle P_{max }}= suma _{i=1}^{k}}min(P_{i+},P_{+i})}.

,
k = liczba kodów, P i + {{displaystyle P_{i+}}

są prawdopodobieństwami wierszy, a P + i {displaystyle P_{+i}}

są prawdopodobieństwami kolumnowymi.
OgraniczeniaEdit
Kappa jest wskaźnikiem, który uwzględnia obserwowaną zgodność w odniesieniu do zgodności bazowej. Osoby prowadzące badania muszą jednak dokładnie rozważyć, czy bazowa zgodność Kappa jest istotna dla danego pytania badawczego. Wartość bazowa Kappa jest często opisywana jako zgodność wynikająca z przypadku, co jest tylko częściowo poprawne. Podstawowa zgodność Kappa to zgodność, której można by się spodziewać w wyniku losowego przydziału, biorąc pod uwagę wielkości określone przez sumy krańcowe kwadratowej tabeli kontyngencji. Zatem Kappa = 0, gdy obserwowany przydział jest najwyraźniej losowy, niezależnie od niezgodności ilościowej ograniczonej przez sumy krańcowe. Jednak w przypadku wielu zastosowań osoby prowadzące badania powinny być bardziej zainteresowane niezgodnością ilościową w sumach krańcowych niż niezgodnością alokacji opisaną przez dodatkowe informacje na przekątnej kwadratowej tabeli kontyngencji. Dlatego też w wielu zastosowaniach wartość bazowa Kappa bardziej rozprasza niż oświeca. Rozważmy następujący przykład:
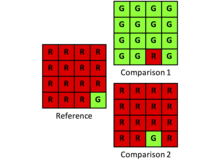
| Referencja | |||
|---|---|---|---|
| G | R | ||
| Porównanie | G | 1 | 14 |
| R | 0 | 1 | |
Proporcja braku zgody wynosi 14/16 lub 0.875. Niezgoda wynika z ilości, ponieważ alokacja jest optymalna. Kappa wynosi 0,01.
| Reference | |||
|---|---|---|---|
| G | R | ||
| Porównanie | G | 0 | 1 |
| R | 1 | 14 | |
Proporcja niezgody wynosi 2/16 lub 0.125. Nieporozumienie wynika z alokacji, ponieważ ilości są identyczne. Kappa wynosi -0,07.
W tym przypadku zgłaszanie braku zgody co do ilości i przydziału ma charakter informacyjny, natomiast Kappa przesłania informacje. Co więcej, Kappa wprowadza pewne wyzwania w obliczeniach i interpretacji, ponieważ Kappa jest współczynnikiem. Możliwe jest, że współczynnik Kappa zwróci niezdefiniowaną wartość z powodu zera w mianowniku. Co więcej, stosunek nie ujawnia swojego licznika ani mianownika. Bardziej informacyjne dla badaczy jest zgłaszanie braku zgody w dwóch komponentach, ilości i alokacji. Te dwa składniki opisują związek między kategoriami w sposób bardziej przejrzysty niż pojedyncza statystyka podsumowująca. Kiedy celem jest dokładność predykcji, badacze mogą łatwiej zacząć myśleć o sposobach poprawy predykcji poprzez wykorzystanie dwóch składowych ilości i alokacji, zamiast jednego współczynnika Kappa.
Niektórzy badacze wyrazili zaniepokojenie tendencją κ do przyjmowania częstotliwości obserwowanych kategorii jako danych, co może sprawić, że nie jest on wiarygodny do pomiaru zgodności w sytuacjach takich jak diagnoza rzadkich chorób. W takich sytuacjach κ ma tendencję do niedoszacowania porozumienia co do rzadkiej kategorii. Z tego powodu κ jest uważane za zbyt konserwatywną miarę porozumienia. Inni kwestionują twierdzenie, że kappa „bierze pod uwagę” przypadkowe porozumienie. Aby zrobić to efektywnie, należałoby stworzyć wyraźny model tego, jak przypadek wpływa na decyzje oceniających. Tak zwana korekta przypadkowości w statystyce kappa zakłada, że kiedy nie ma całkowitej pewności, oceniający po prostu zgadują – jest to bardzo nierealistyczny scenariusz.
.