A 
macierz 
jest macierzą ortogonalną, jeżeli
 |
(1)
|
gdzie 
jest transpozycją 
a 
jest macierzą tożsamości. W szczególności, macierz ortogonalna jest zawsze odwracalna, a
 |
(2)
|
W formie składowej,
 |
(3)
|
Zależność ta sprawia, że macierze ortogonalne są szczególnie łatwe do obliczania, ponieważ operacja transpozycji jest znacznie prostsza niż obliczanie odwrotności.
Na przykład,
 |
 |
 |
(4)
|
 |
 |
 |
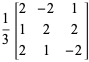(5)
|
Są macierzami ortogonalnymi.
Macierz 
może być testowana, aby sprawdzić, czy jest ortogonalna w Wolfram Language za pomocą OrthogonalMatrixQ.
Rzędy macierzy ortogonalnej są podstawą ortonormalną. To znaczy, że każdy rząd ma długość jeden i są wzajemnie prostopadłe. Podobnie, kolumny są również ortonormalną bazą. W rzeczywistości, biorąc pod uwagę dowolną bazę ortonormalną, macierz, której wiersze są tą bazą, jest macierzą ortogonalną. Automatycznie jest też tak, że kolumny są kolejną podstawą ortogonalną.
Macierze ortogonalne to dokładnie te macierze, które zachowują iloczyn wewnętrzny
 |
(6)
|
A także, wyznacznikiem 
jest albo 1 albo 
. Jako podzbiór 
, macierze ortogonalne nie są połączone, ponieważ wyznacznik jest funkcją ciągłą. Zamiast tego istnieją dwa składniki odpowiadające temu, czy wyznacznik wynosi 1 czy 
. Macierze ortogonalne z 
są rotacjami, a taka macierz nazywana jest specjalną macierzą ortogonalną.
Iloczyn dwóch macierzy ortogonalnych jest kolejną macierzą ortogonalną. Ponadto, odwrotność macierzy ortogonalnej jest macierzą ortogonalną, podobnie jak macierz tożsamości. Stąd zbiór macierzy ortogonalnych tworzy grupę, zwaną grupą ortogonalną 
.
.