Wprowadzenie
Analiza regresji jest powszechnie stosowana do modelowania zależności pomiędzy pojedynczą zmienną zależną Y a jednym lub większą liczbą predyktorów. Gdy mamy jeden predyktor, nazywamy to „prostą” regresją liniową:
E = β0 + β1X
To znaczy, że wartość oczekiwana Y jest funkcją prostoliniową X. Bety są wybierane przez wybranie linii, która minimalizuje odległość podniesioną do kwadratu między każdą wartością Y a linią najlepszego dopasowania. Bety są wybierane tak, aby zminimalizować to wyrażenie:
∑i (yi – (β0 + β1X))2
Pouczającą grafika, którą znalazłem w Internecie

Źródło: http://www.unc.edu/~nielsen/soci709/m1/m1005.gif
Gdy mamy więcej niż jeden predyktor, nazywamy to wielokrotną regresją liniową:
Y = β0 + β1X1+ β2X2+ β2X3+… + βkXk
Wartości dopasowane (tj, wartości przewidywane) są zdefiniowane jako te wartości Y, które są generowane, jeśli wpiszemy nasze wartości X do naszego dopasowanego modelu.
Reszty są dopasowanymi wartościami minus rzeczywiste obserwowane wartości Y.
Tutaj znajduje się przykład regresji liniowej z dwoma predyktorami i jednym wynikiem:
Zamiast „linii najlepszego dopasowania”, istnieje „płaszczyzna najlepszego dopasowania.”
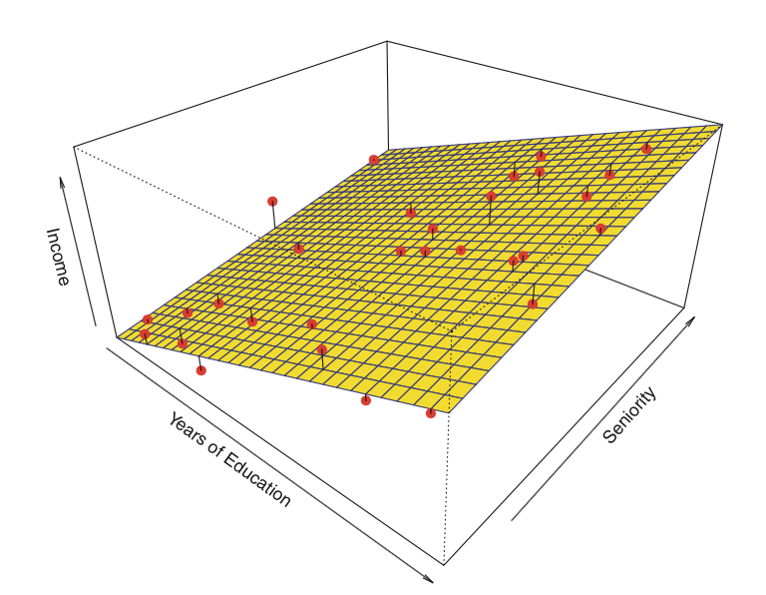
Źródło: James et al. Introduction to Statistical Learning (Springer 2013)
Z modelem regresji liniowej związane są cztery założenia:
- Liniowość: Zależność między X a średnią Y jest liniowa.
- Homoscedastyczność: Wariancja reszt jest taka sama dla każdej wartości X.
- Niezależność: Obserwacje są od siebie niezależne.
- Normalność: Dla dowolnej stałej wartości X, Y ma rozkład normalny.
Prześledzimy, jak ocenić te założenia w dalszej części modułu.
Zacznijmy od prostej regresji. W R, modele są zwykle dopasowywane przez wywołanie funkcji dopasowującej model, w naszym przypadku lm(), z obiektem „formula” opisującym model i obiektem „data.frame” zawierającym zmienne użyte we wzorze. Typowe wywołanie może wyglądać tak
> myfunction <- lm(formuła, dane, …)
i zwróci dopasowany obiekt modelu, tutaj przechowywany jako myfunction. Ten dopasowany model może być następnie wydrukowany, podsumowany lub zwizualizowany; co więcej, dopasowane wartości i reszty mogą być wyodrębnione, a my możemy dokonać przewidywań na nowych danych (wartości X) obliczonych przy użyciu funkcji takich jak summary(), residuals(),predict(), itp. Następnie przyjrzymy się, jak dopasować prostą regresję liniową.
powrót do góry | poprzednia strona | następna strona