Nella nostra lezione precedente, abbiamo studiato come usare la Regola di Cramer con due variabili. Il nostro obiettivo qui è quello di espandere l’applicazione della Regola di Cramer a tre variabili di solito in termini di ¤large{x}, ¤large{y} e ¤large{z}. Andrò oltre cinque (5) esempi lavorati per aiutarti a familiarizzare con questo concetto.
Per fare bene questo argomento, devi avere un’idea su come trovare il determinante di una matrice 3⨉3. Quindi, questo è ciò che faremo per prima cosa. Pronti?
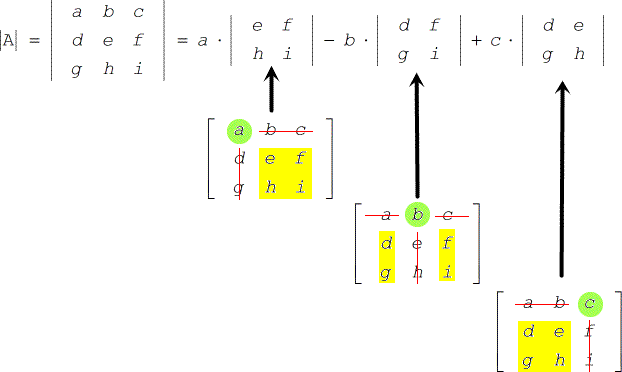
Formula per trovare il determinante di una matrice 3⨉3
- Data una matrice 3⨉3

- Il suo determinante può essere calcolato usando la seguente formula.
Facciamo un rapido esempio di questo.
Trovare il determinante della matrice A
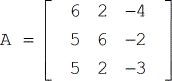
Soluzione: Assicuratevi di seguire attentamente la formula su come trovare il determinante di una matrice 3×3, come mostrato sopra. Ancora di più, non abbiate fretta quando eseguite le operazioni aritmetiche richieste in ogni passo. Questo è il punto in cui di solito si verificano errori comuni, ma può essere evitato. Quando lo fate bene, la vostra soluzione dovrebbe essere simile a quella qui sotto.
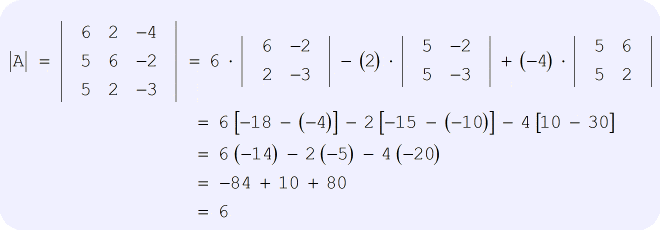
Ora, è il momento di esaminare la procedura su come utilizzare la Regola di Cramer in un sistema lineare che coinvolge tre variabili.
Regole di Cramer per sistemi di equazioni lineari con tre variabili
- Dato un sistema lineare

- etichettatura di ciascuna delle quattro matrici
matrice dei coefficienti:
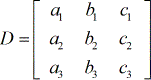
X – matrice:
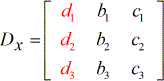
Y – matrice:
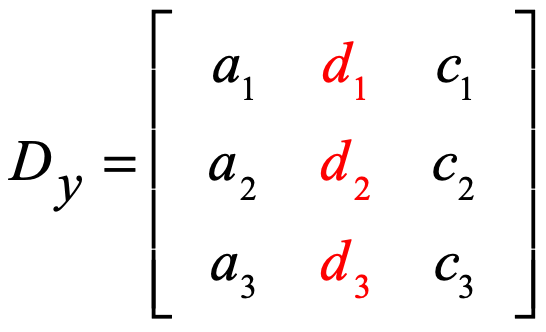
Z – matrice:
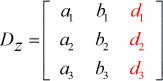
- Per risolvere x:
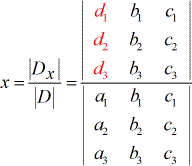
- Per risolvere y:
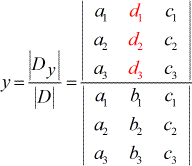
- Per risolvere z:
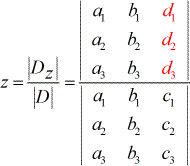
Cose da osservare dalla configurazione di cui sopra:
1) I coefficienti delle variabili x, y e z fanno uso di pedici a, b e c, rispettivamente. Mentre i termini costanti usano la pedice d.
2) I denominatori per trovare i valori di x, y e z sono tutti uguali, che è il determinante della matrice dei coefficienti (coefficienti provenienti dalle colonne di x, y e z).
3) Per risolvere x, i coefficienti della colonna x sono sostituiti dalla colonna costante (in rosso).
4) Per risolvere y, i coefficienti della colonna y sono sostituiti dalla colonna costante (in rosso).
5) Allo stesso modo, per risolvere z, i coefficienti della colonna z sono sostituiti dalla colonna costante (in rosso).
Esempi di come risolvere sistemi di equazioni lineari con tre variabili usando la regola di Cramer
Esempio 1: Risolvere il sistema con tre variabili con la regola di Cramer.
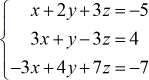
Dal sistema di equazioni lineari dato, costruirò le quattro matrici che saranno utilizzate per risolvere i valori di \large{color{green}x}, \large{color{green}y} e \large{color{green}z}.
Utilizza la guida sopra per impostare correttamente queste matrici speciali.
- matrice dei coefficienti
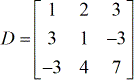
- X – matrice
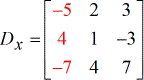
- Y – matrice
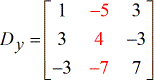
- Z – matrice
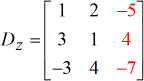
In seguito, risolverò il determinante di ogni matrice. Per fare questo, posso risolvere manualmente il determinante di ogni matrice sulla carta usando la formula fornita sopra. Può essere noioso, ma va bene perché le buone abilità matematiche si sviluppano facendo molti problemi.
I valori dei determinanti sono elencati qui sotto.
Determinanti di ogni matrice:
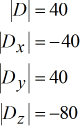
Le risposte finali o le soluzioni sono facilmente calcolate una volta trovati tutti i determinanti richiesti.
Valori risolti per \large{color{green}x}, \large{color{green}y} e \large{color{green}z}.
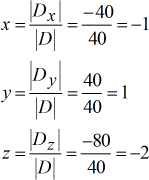
La risposta finale scritta in notazione puntiforme è \color{blu} \left( {x,y,z} \right) = \left( { – 1,1, – 2} \right).
Esempio 2: Risolvere il sistema a tre variabili con la Regola di Cramer.
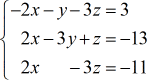
In realtà considero la matrice dei coefficienti come la matrice “primaria” perché le altre tre matrici sono derivate da essa. Per esempio, la matrice x è solo la matrice “primaria” con la colonna x sostituita dalla colonna della costante (in rosso). Si può osservare che lo stesso schema è applicato nella costruzione delle altre matrici: y e z.
- matrice coefficiente
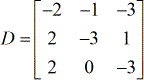
- X – matrice
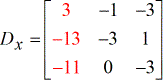
- Y – matrice
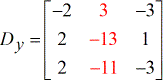
- Z – matrice
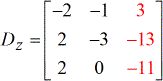
Dopo aver risolto il determinante di ogni matrice, li ho tutti scritti.
Determinanti di ogni matrice:
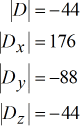
I valori di x, y e z sono calcolati come segue. Notate che x si ottiene prendendo il determinante della matrice x diviso il determinante della matrice dei coefficienti. Questa regola vale per il resto.
Valori risolti per x, y e z.
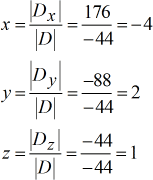
La nostra risposta finale è \color{blu}\sinistra( {x,y,z} destra) = \sinistra( { – \,4,2,1} destra).
Esempio 3: Risolvere il sistema a tre variabili con la regola di Cramer.
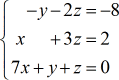
Questo problema è molto più facile dei primi due esempi per la presenza di voci zero nelle colonne x, y e costante. Lo vedete? Quando abbiamo voci zero in una matrice, il calcolo della sua determinazione è drammaticamente semplificato.
In effetti, man mano che si aumenta il numero di zeri in una matrice quadrata, il lavoro fatto per trovare il suo determinante si riduce notevolmente.
Ecco le matrici estratte dal sistema di equazioni lineari.
- matrice determinante
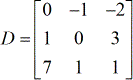
- X – matrice
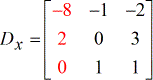
- Y – matrice
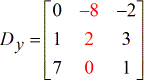
- Z – matrice
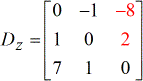
Solvendo i loro determinanti, ho ottenuto i seguenti valori.
Determinanti di ogni matrice:
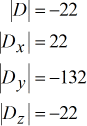
Questo ci porta a impostare e calcolare facilmente le risposte finali.
I valori risolti per \large{color{green}x}, \large{color{green}y} e \large{color{green}z}.
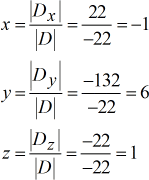
La risposta finale è \color{blu} \left( {x,y,z} \right) = \left( { – \,1,6,1} \right).
Esempio 4: Risolvere il sistema a tre variabili con la Regola di Cramer
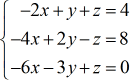
Scrivi le quattro matrici speciali.
- matrice dei coefficienti
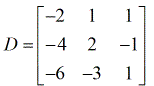
- X – matrice
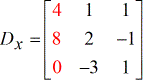
- Y – matrice
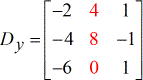
- Z – matrice
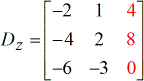
Valutiamo ogni matrice per trovare il suo determinante.
Questi sono i determinanti di ogni matrice:
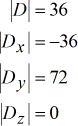
Utilizzare la regola di Cramer per ottenere le seguenti soluzioni.
Valori risolti per \large{color{green}x}, \large{color{green}y} e \large{color{green}z}.
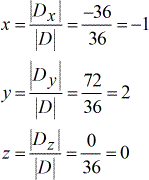
La risposta finale è \color{blu}\sinistra( {x,y,z} \destra) = \sinistra( { – \,1,2,0} \destra).
Esempio 5: Risolvere il sistema a tre variabili con la regola di Cramer
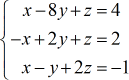
Facciamo un ultimo esempio! Spero che a questo punto tu abbia fatto abbastanza pratica su come risolvere sistemi con tre variabili usando la Regola di Cramer.
Ti suggerisco di risolvere prima questo su carta e poi tornare per confrontare la tua risposta. Non preoccuparti, nessuno sta guardando. 👀 Quando sei pronto, scorri in basso per vedere la soluzione.

Costruisci le quattro matrici speciali.
- matrice dei coefficienti
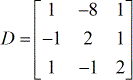
- X – matrice
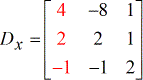
- Y – matrice
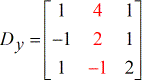
- Z – matrice
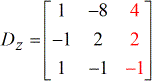
Trovare il determinante di ogni matrice quadrata.
Determinanti di ogni matrice
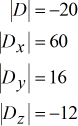
Solvere per x, y e z usando la formula data.
Valori risolti per \large{color verde}x}, \large{color verde}y} e \large{color verde}z}.
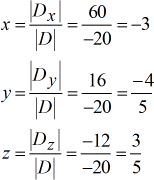
Fatto! La risposta finale in forma puntiforme è \color{blu} \sinistra( {x,y,z} \destra) = {grandioso { {sinistra( { – \,3, – {4 \su 5},{3 \su 5}} \destra)}}.
Pratica con i fogli di lavoro
Ti potrebbe interessare anche:
Regola di Cramer 2×2