Introduzione
L’analisi di regressione è comunemente usata per modellare la relazione tra una singola variabile dipendente Y e uno o più predittori. Quando abbiamo un solo predittore, chiamiamo questa regressione lineare “semplice”:
E = β0 + β1X
Quindi, il valore atteso di Y è una funzione della linea retta di X. I beta sono selezionati scegliendo la linea che minimizza la distanza al quadrato tra ogni valore Y e la linea di miglior adattamento. I beta sono scelti in modo da minimizzare questa espressione:
∑i (yi – (β0 + β1X))2
Un istruttivo grafico che ho trovato su Internet

Fonte: http://www.unc.edu/~nielsen/soci709/m1/m1005.gif
Quando abbiamo più di un predittore, la chiamiamo regressione lineare multipla:
Y = β0 + β1X1+ β2X2+ β2X3+… + βkXk
I valori adattati (cioè, i valori predetti) sono definiti come quei valori di Y che sono generati se inseriamo i nostri valori X nel nostro modello adattato.
I residui sono i valori adattati meno i valori reali osservati di Y.
Ecco un esempio di regressione lineare con due predittori e un risultato:
Invece della “linea di miglior adattamento”, esiste un “piano di miglior adattamento”
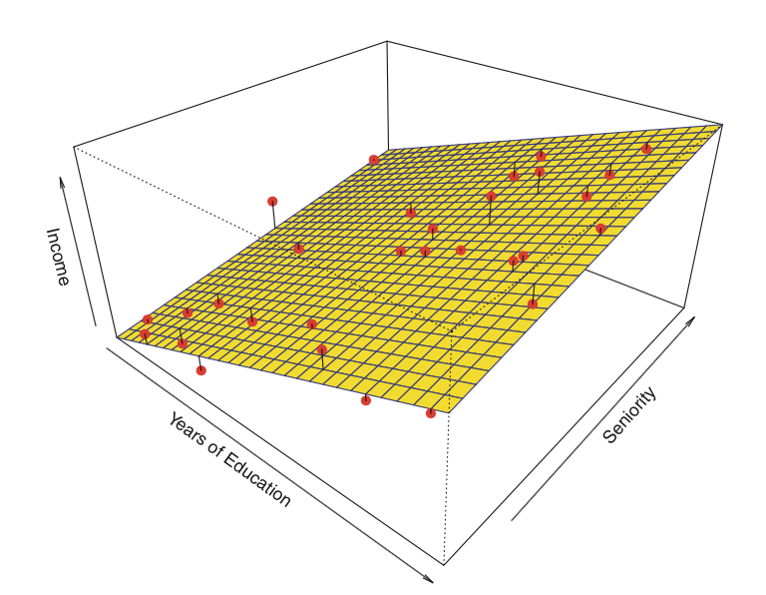
Fonte: James et al. Introduction to Statistical Learning (Springer 2013)
Ci sono quattro ipotesi associate ad un modello di regressione lineare:
- Linearità: La relazione tra X e la media di Y è lineare.
- Omoscedasticità: La varianza dei residui è la stessa per qualsiasi valore di X.
- Indipendenza: Le osservazioni sono indipendenti l’una dall’altra.
- Normalità: Per qualsiasi valore fisso di X, Y è normalmente distribuito.
Rivedremo come valutare queste ipotesi più avanti nel modulo.
Iniziamo con una semplice regressione. In R, i modelli sono tipicamente adattati chiamando una funzione di model-fitting, nel nostro caso lm(), con un oggetto “formula” che descrive il modello e un oggetto “data.frame” contenente le variabili usate nella formula. Una tipica chiamata può assomigliare a
> myfunction <- lm(formula, dati, …)
e restituirà un oggetto modello montato, qui memorizzato come myfunction. Questo modello adattato può essere successivamente stampato, riassunto o visualizzato; inoltre, i valori adattati e i residui possono essere estratti, e possiamo fare previsioni su nuovi dati (valori di X) calcolati utilizzando funzioni come summary(), residuals(),predict(), ecc. In seguito, vedremo come applicare una semplice regressione lineare.
torna all’inizio | pagina precedente | pagina successiva